AD is a diameter of a circle and AB is a chord. If AD = 34 cm and AB = 30 cm, then the distance of AB from the center of circle is

1. 17 cm

2. 15 cm

3. 4 cm

4. 8 cm

Let OM be the distance of AB from the center of the circle.

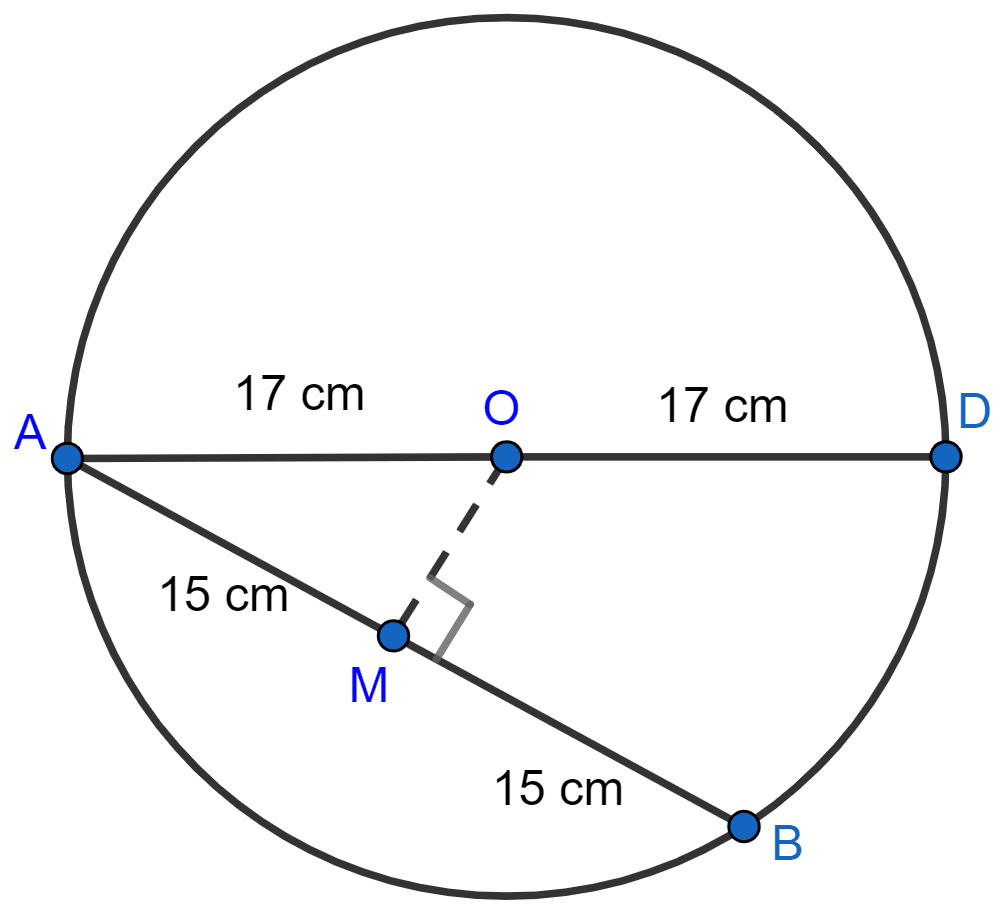
Since diameter = 34 cm, so radius = $\dfrac{34}{2}$ = 17 cm.

Since, the perpendicular to a chord from the centre of the circle bisects the chord,

∴ AM = MB = 15 cm.

In right triangle OAM,

⇒ OA² = AM² + OM² (By pythagoras theorem)

⇒ OM² = OA² - AM²

⇒ OM² = 17² - 15²

⇒ OM² = 289 - 225

⇒ OM² = 64

⇒ OM = $\sqrt{64}$ = 8 cm.

Hence, Option 4 is the correct option.