Mathematics
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that :
(i) ABCD is a square
(ii) diagonal BD bisects ∠B as well as ∠D.
Rectilinear Figures
7 Likes
Answer
Rectangle ABCD is shown in the figure below:

(i) Given :
ABCD is a rectangle and AC bisects ∠A and ∠C.
⇒ ∠DAC = ∠CAB ….(1)
⇒ ∠DCA = ∠BCA …..(2)
We know that,
Opposite sides of a rectangle are parallel and equal.
From figure,
AD || BC and AC is transversal,
⇒ ∠DAC = ∠BCA ……….(3) (Alternate interior angles are equal)
From equations (1) and (3), we get :
⇒ ∠CAB = ∠BCA ……(4)
In △ ABC,
⇒ ∠CAB = ∠BCA
We know that,
Sides opposite to equal angles are equal.
⇒ BC = AB …..(5)
We know that,
Opposite sides of a rectangle are equal.
⇒ BC = AD ………(6)
⇒ AB = DC ………(7)
From equation (5), (6) and (7), we get :
⇒ AB = BC = CD = AD.
Since,
ABCD is a rectangle and all the sides are equal. Hence, ABCD is a square.
Hence, proved that ABCD is a square.
(ii) Join BD.
In Δ BCD,
⇒ BC = CD (Sides of a square are equal to each other)
⇒ ∠CDB = ∠CBD (Angles opposite to equal sides are equal) ….. (8)
⇒ ∠CDB = ∠ABD (Alternate interior angles are equal) ….. (9)
From equations (8) and (9), we get :
⇒ ∠CBD = ∠ABD
∴ BD bisects ∠B.
From figure,
⇒ ∠CBD = ∠ADB (Alternate interior angles are equal) …..(10)
From equations (8) and (10), we get :
⇒ ∠ADB = ∠CDB
∴ BD bisects ∠D.
Hence, proved that diagonal BD bisects ∠B as well as ∠D.
Answered By
3 Likes
Related Questions
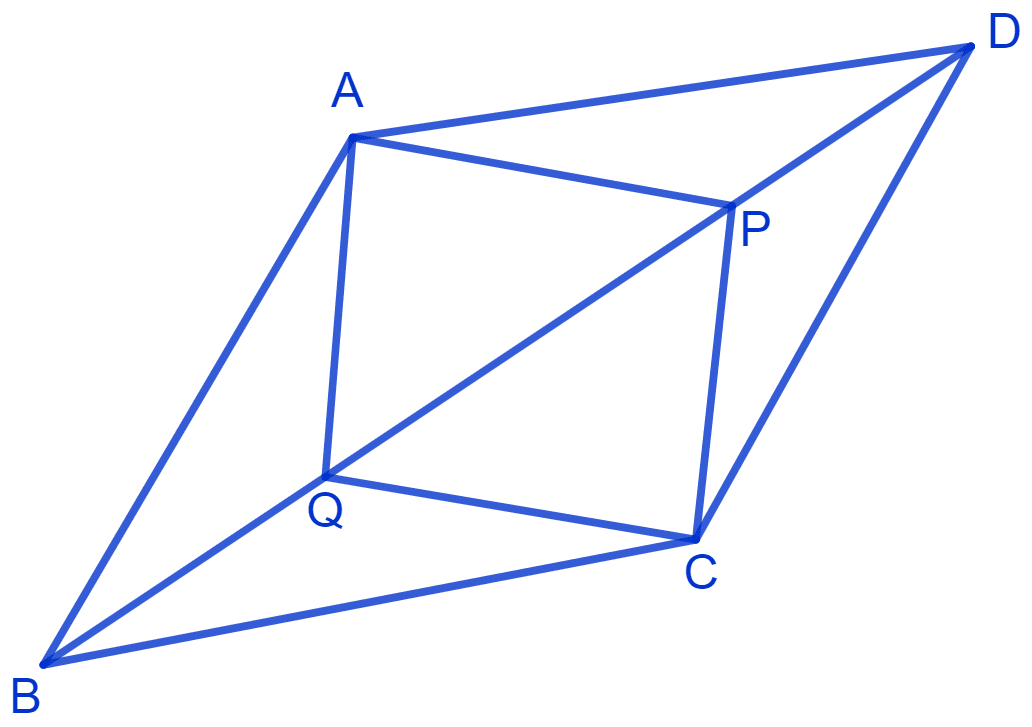
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ see Fig. Show that:
(i) Δ APD ≅ Δ CQB
(ii) AP = CQ
(iii) Δ AQB ≅ Δ CPD
(iv) AQ = CP
(v) APCQ is a parallelogram
Show that the diagonals of a square are equal and bisect each other at right angles.
Diagonal AC of a parallelogram ABCD bisects ∠A. Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
(Ex.8.1Q3.png)
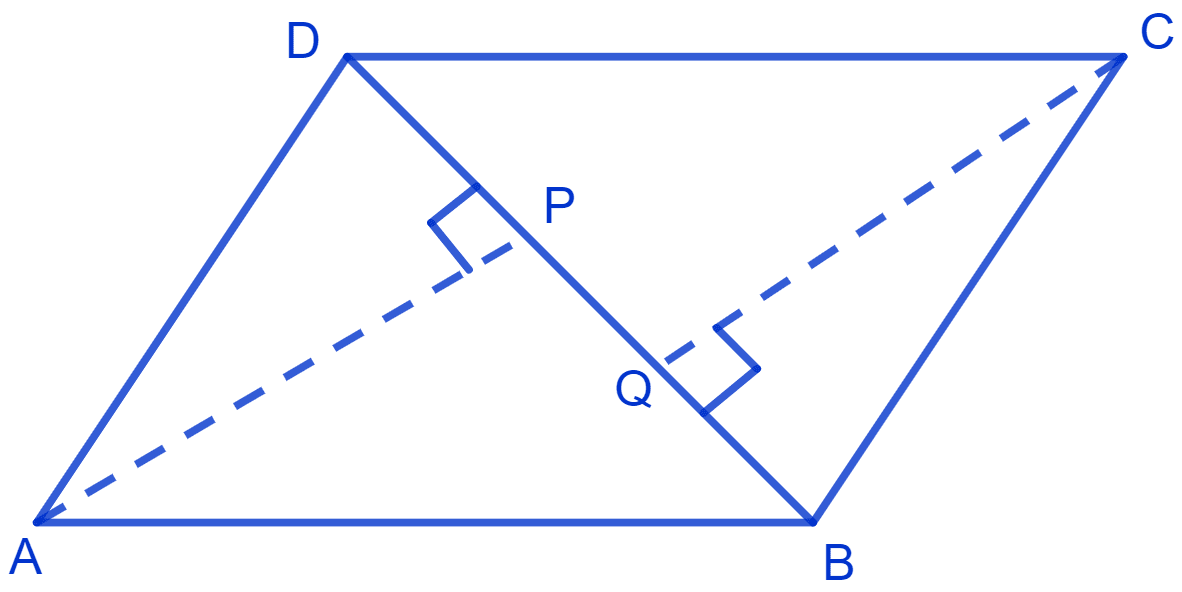
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD. Show that
(i) Δ APB ≅ Δ CQD
(ii) AP = CQ