Mathematics
ABCD is a rectangle and P is the mid-point of AB. DP is produced to meet CB at Q. Prove that the area of rectangle ABCD = area of ∆DQC.
Theorems on Area
14 Likes
Answer
In ∆APD and ∆PQB,
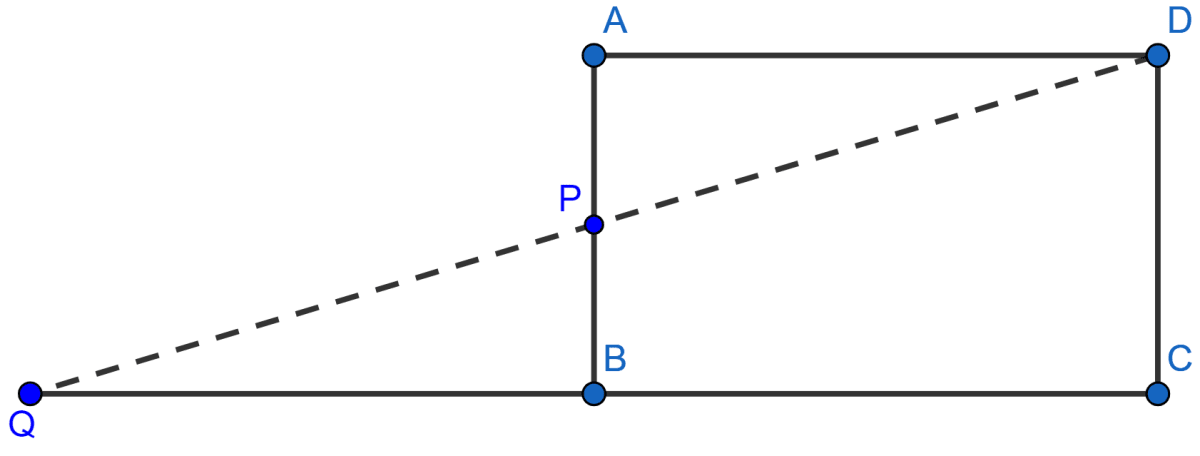
AP = BP [Since P is the mid-point of AB]
∠DAP = ∠QBP [each angle is 90° as ABCD is a rectangle]
∠APD = ∠BPQ [Vertically opposite angles are equal]
So, ∆APD ≅ ∆PQB [By using ASA axiom]
So, area of ∆APD = area of ∆PQB …….(i) (As both triangles are congruent.)
From figure,
area of rectangle ABCD = area of ∆APD + area of quad. PBCD
= area of ∆PQB + area of quad. PBCD ……(From i)
= area of ∆DQC.
Hence, proved that area of rectangle ABCD = area of ∆DQC..
Answered By
10 Likes
Related Questions
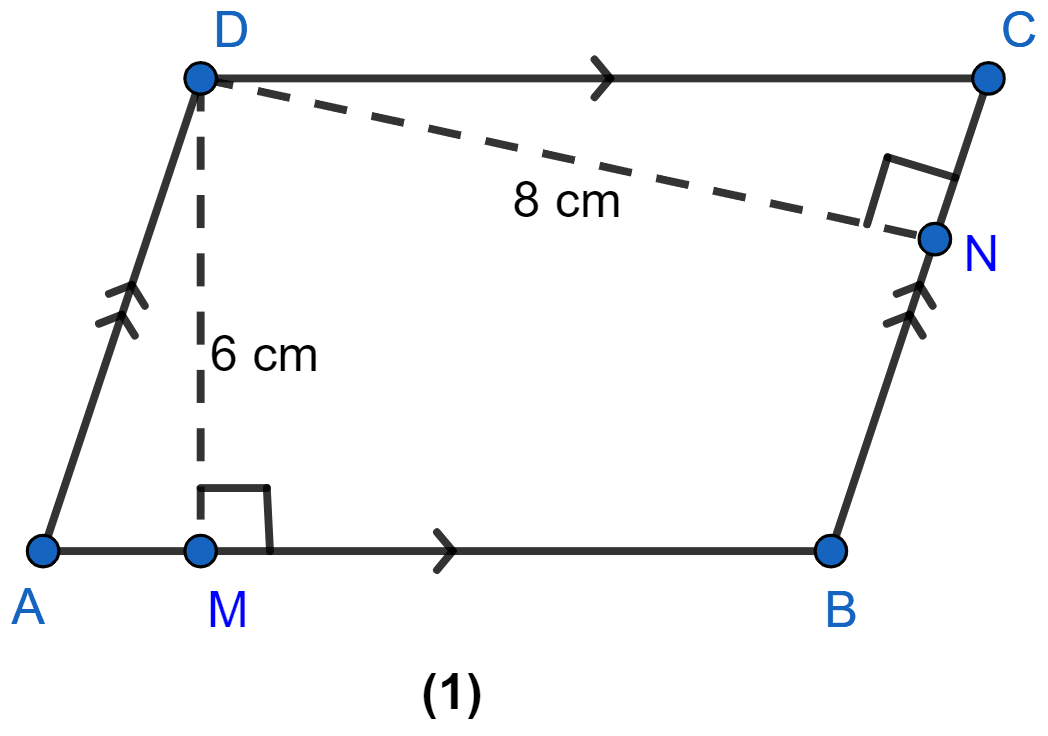
In figure (1) given below, the perimeter of the parallelogram is 42 cm. Calculate the lengths of the sides of the parallelogram.
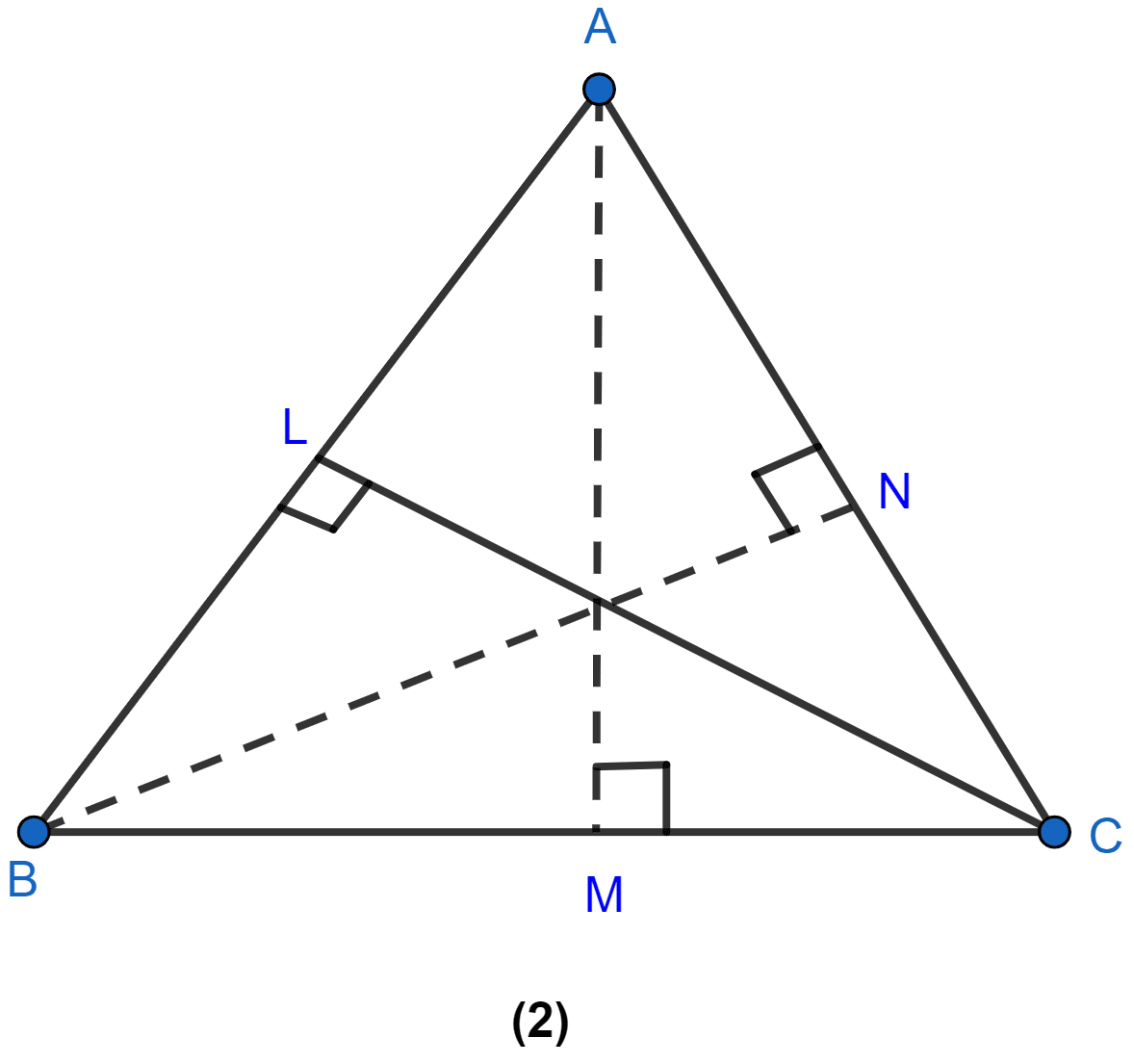
In the figure (2) given below, the perimeter of ∆ABC is 37 cm. If the lengths of the altitudes AM, BN and CL are 5x, 6x, and 4x respectively, calculate the lengths of the sides of ∆ABC.
Any point D is taken on the side BC of a ∆ABC and AD is produced to E such that AD = DE, prove that area of ∆BCE = area of ∆ABC.
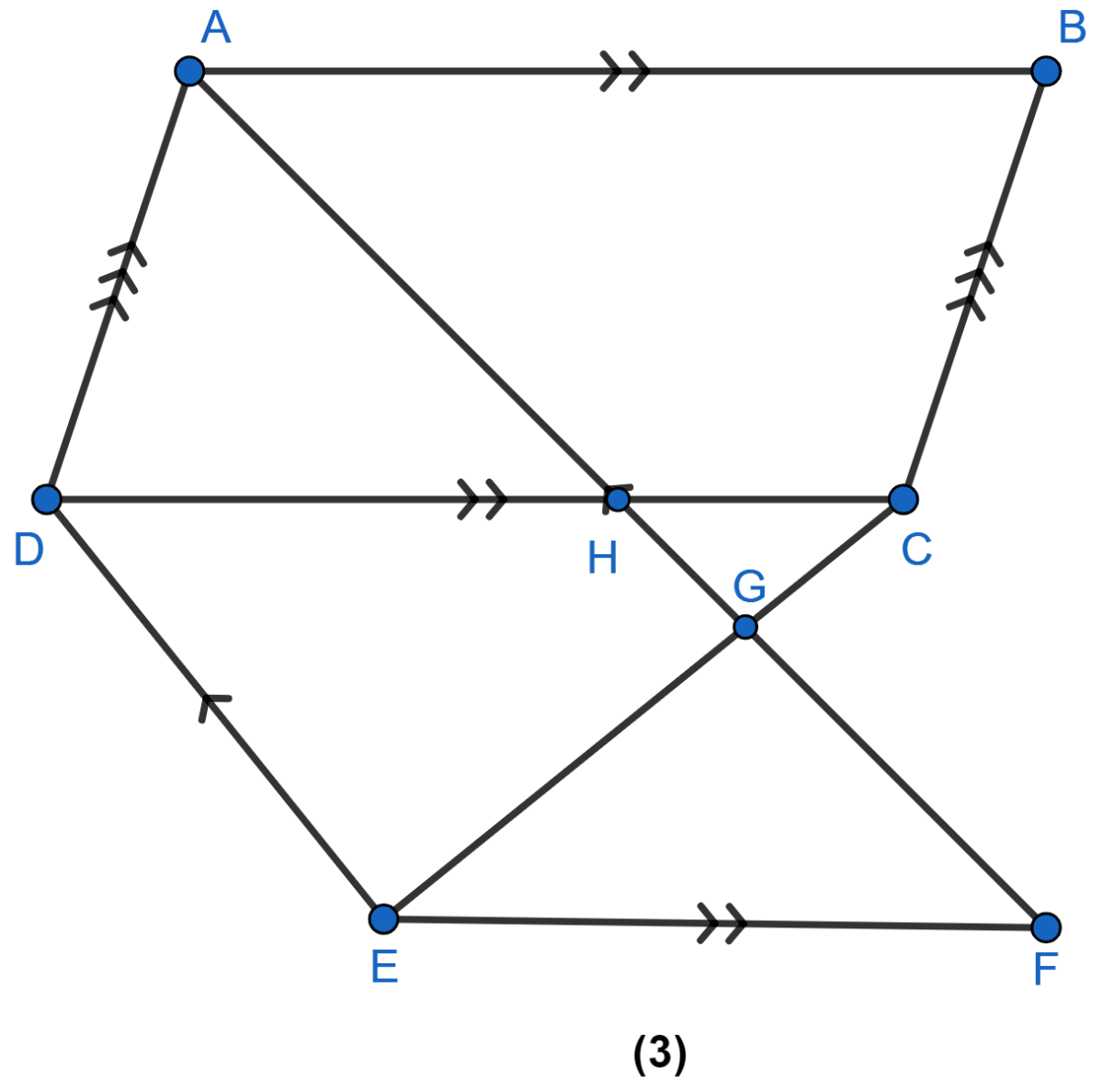
In figure (3) given below, AB || DC || EF, AD || BE and DE || AF. Prove that the area of DEFH is equal to the area of ABCD.