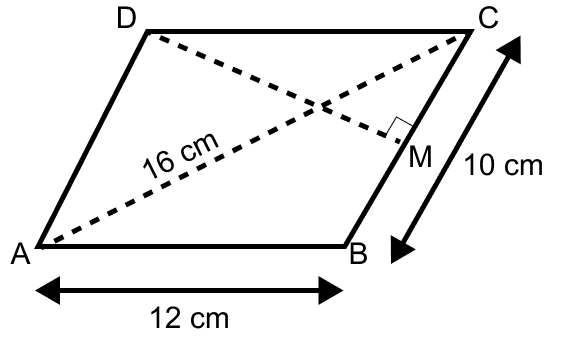
ABCD is a parallelogram with sides AB = 12 cm, BC = 10 cm and diagonal AC = 16 cm. Find the area of the parallelogram. Also find the distance between its shorter sides.

In triangle ABC,

Let,

BC = a = 10 cm, AC = b = 16 cm and AB = c = 12 cm.

We know that,

Semi-perimeter (s) = $\dfrac{a + b + c}{2}$

= $\dfrac{10 + 16 + 12}{2} = \dfrac{38}{2}$ = 19 cm.

By Heron's formula,

$\text{Area of triangle } = \sqrt{s(s - a)(s - b)(s - c)} \\[1em] = \sqrt{19(19 - 10)(19 - 16)(19 - 12)} \\[1em] = \sqrt{19 \times 9 \times 3 \times 7} \\[1em] = \sqrt{3591} \\[1em] = 59.9 \text{ cm}^2.$

We know that,

Diagonal of a parallelogram divides it into two triangles of equal area.

∴ Area of triangle ABC = Area of triangle ADC

∴ Area of parallelogram = 2 × Area of triangle ABC.

= 2 × 59.9

= 119.8 cm².

Let DM be the distance between the shorter sides of the parallelogram.

By formula,

Area of parallelogram = base × height = BC × DM

Substituting the values we get,

⇒ 119.8 = 10 × DM

⇒ DM = $\dfrac{119.8}{10}$

⇒ DM = 11.98 cm.

Hence, the distance between shorter sides = 11.98 cm and area of parallelogram = 119.8 cm².