Mathematics
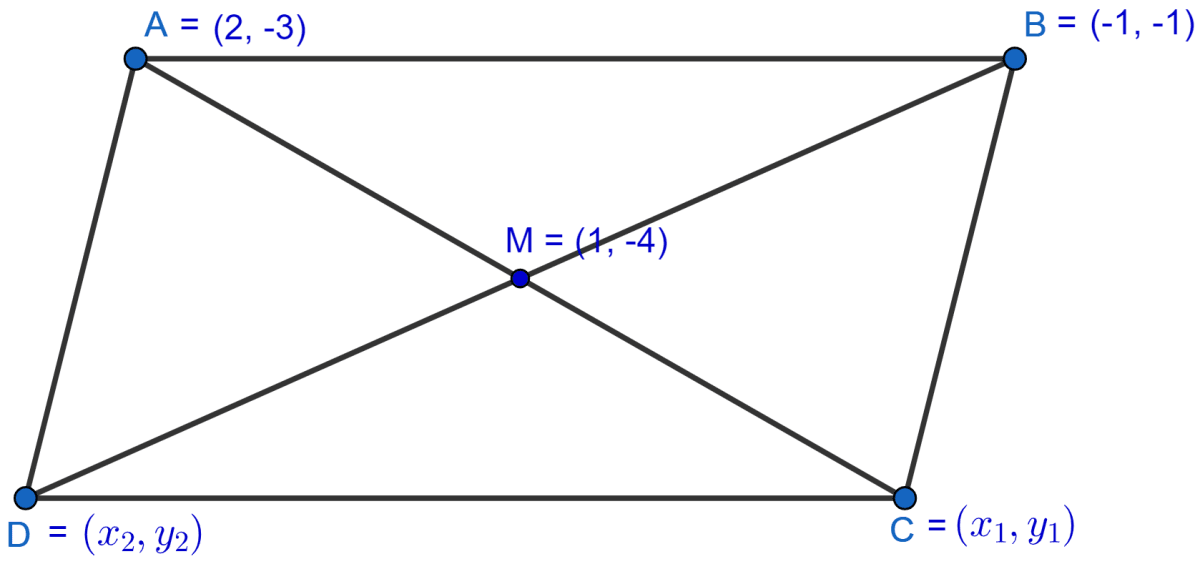
ABCD is a parallelogram whose vertices A and B have coordinates (2, -3) and (-1, -1) respectively. If the diagonals of the parallelogram meet at the point M(1, -4), find the coordinates of C and D. Hence, find the perimeter of the parallelogram.
Section Formula
30 Likes
Answer
Coordinates of A are (2, -3) and B (-1, -1).
Since, M is the point where diagonals meet, hence it is midpoint of AC and BD.
Let coordinates of C and D be (x1, y1) and (x2, y2).
When M(1, -4) is the midpoint of AC then by midpoint formula,
∴ Coordinates of C are (0, -5)
When M(1, -4) is the midpoint of BD then by midpoint formula,
∴ Coordinates of D are (3, -7).
By distance formula, the length of AB is,
By distance formula, the length of BC is,
Perimeter of parallelogram ABCD = 2(AB + BC) =
Hence, the coordinates of C and D are (0, -5) and (3, -7) respectively. The perimeter of parallelogram ABCD is units.
Answered By
22 Likes
Related Questions
Determine the ratio in which the line 2x + y - 4 = 0 divide the line segment joining the points A(2, -2) and B(3, 7). Also find the coordinates of the point of the division.
ABCD is a parallelogram. If the coordinates of A, B and D are (10, -6), (2, -6) and (4, -2) respectively, find the coordinates of C.
Given O (0, 0), P(1, 2), S(-3, 0). P divides OQ in the ratio 2 : 3 and OPRS is a parallelogram.
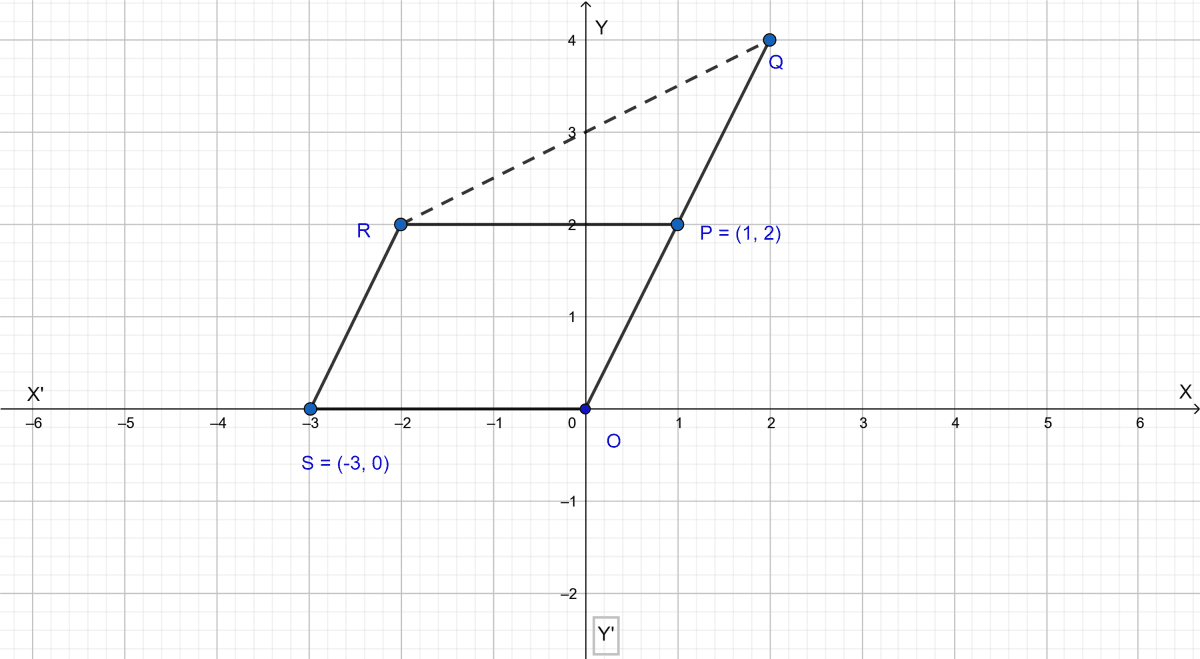
Find :
(i) the coordinates of Q.
(ii) the coordinates of R.
(iii) the ratio in which RQ is divided by the x-axis.
If A(5, -1), B(-3, -2) and C(-1, 8) are the vertices of a triangle ABC, find the length of the median through A and the coordinates of the centroid of triangle ABC.