Mathematics
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Circles
13 Likes
Answer
Cyclic quadrilateral ABCD is shown in the figure below:
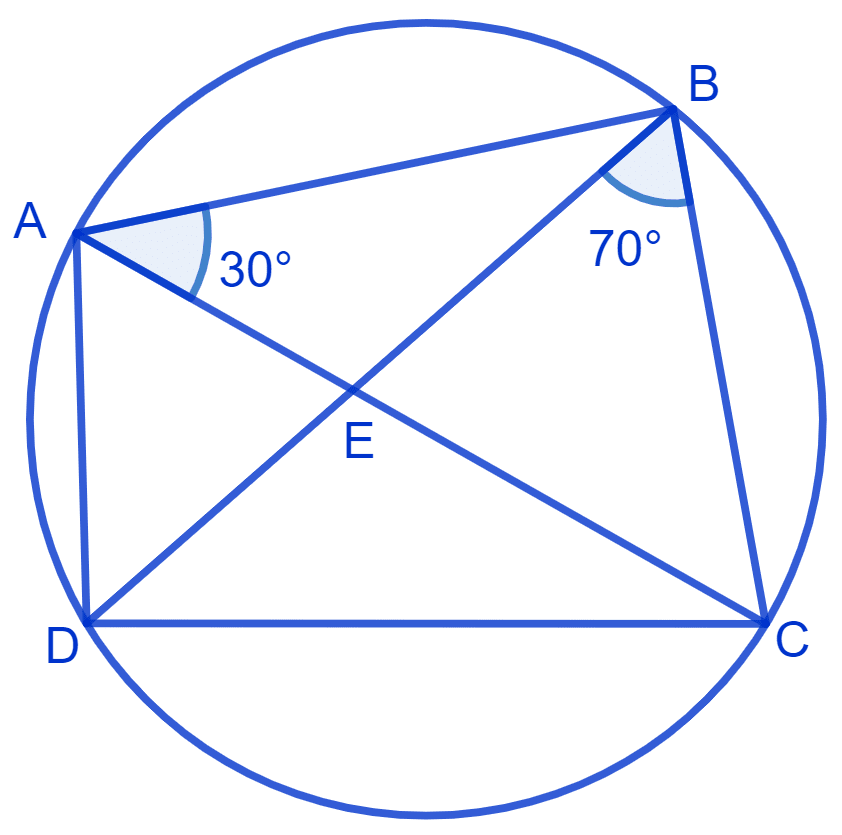
∠CAD = ∠CBD = 70° (Angles in the same segment are equal)
From figure,
⇒ ∠BAD = ∠CAB + ∠DAC
⇒ ∠BAD = 30° + 70°
⇒ ∠BAD = 100°.
Since ABCD is a cyclic quadrilateral, the sum of opposite angles of a cyclic quadrilateral is 180°.
⇒ ∠BAD + ∠BCD = 180°
⇒ ∠BCD = 180° - ∠BAD
⇒ ∠BCD = 180° - 100° = 80°
Given, AB = BC
In △ ABC,
⇒ ∠BCA = ∠BAC = 30° (Angles opposite to equal sides are equal)
From figure,
⇒ ∠ECD = ∠BCD - ∠BCA
⇒ ∠ECD = 80° - 30° = 50°.
Hence, ∠BCD = 80° and ∠ECD = 50°.
Answered By
8 Likes
Related Questions
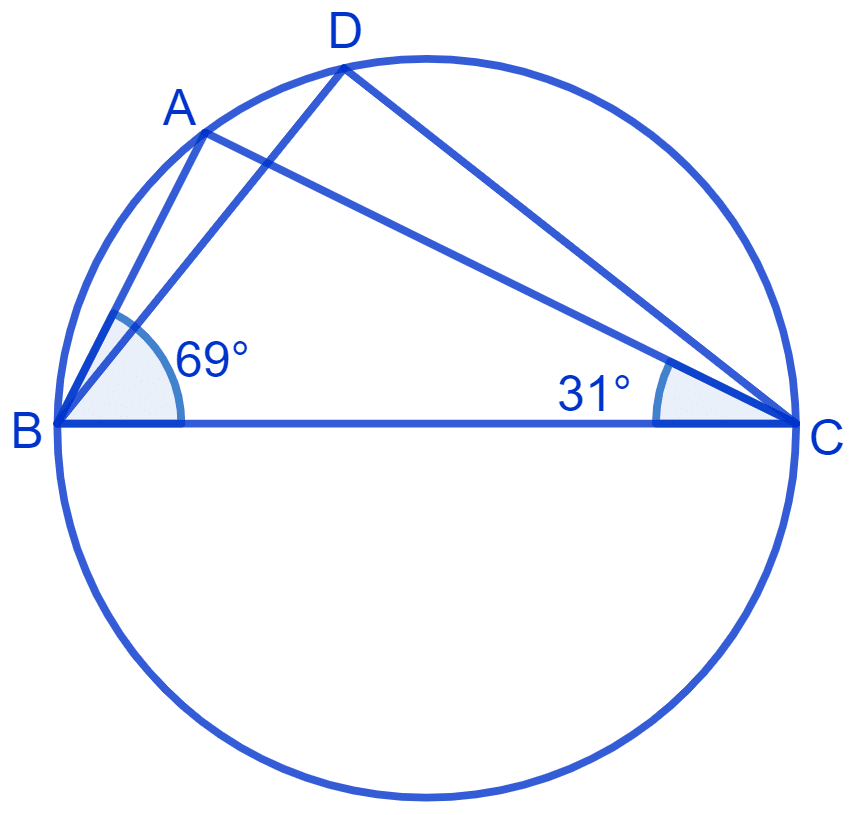
In Fig. ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
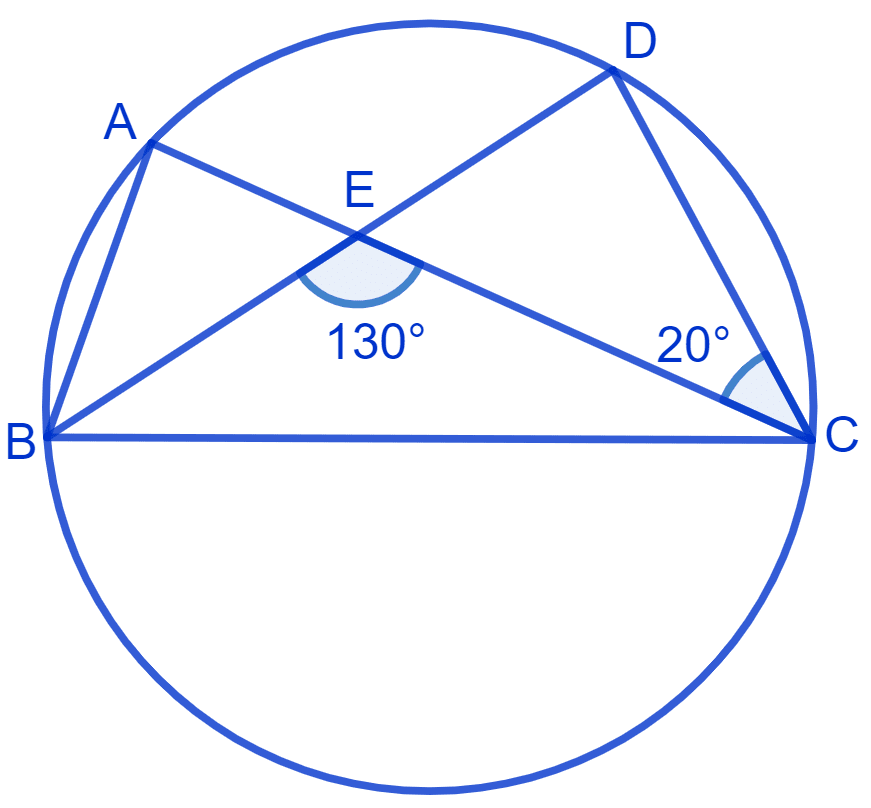
In Fig. A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.