Mathematics
ABC is an isosceles triangle in which AB = AC. P is any point in the interior of △ABC such that ∠ABP = ∠ACP. Prove that
(a) BP = CP
(b) AP bisects ∠BAC.
Answer
Below figure shows the isosceles triangle ABC with the points marked:
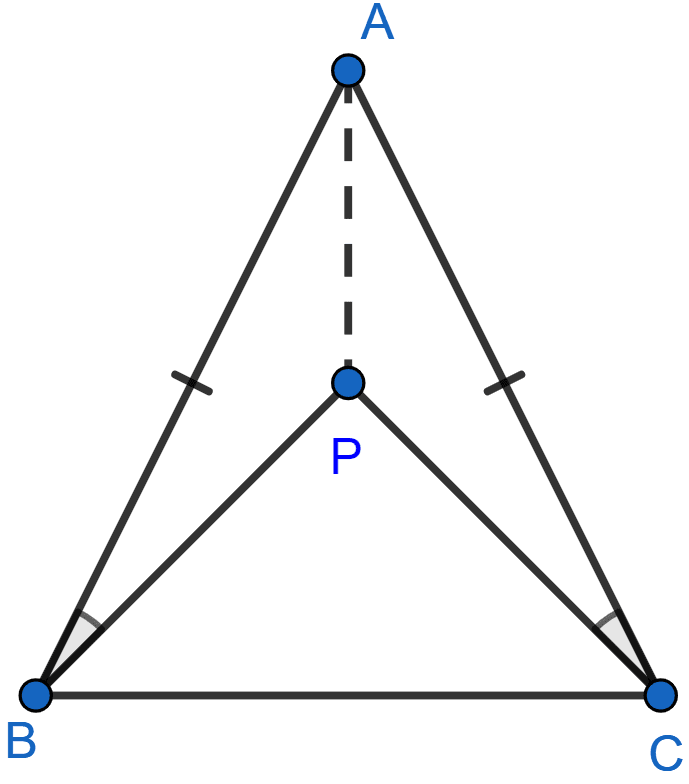
(a) Given,
AB = AC
∴ ∠B = ∠C ……..(i)
Given, ∠ABP = ∠ACP ……..(ii)
Subtracting (ii) from (i) we get,
∠B - ∠ABP = ∠C - ∠ACP
∠PBC = ∠PCB.
∴ BP = CP (As sides opposite to equal angles are equal)
Hence, proved that BP = CP.
(b) We know that,
BP = CP (Proved)
AB = AC (Given)
∠ABP = ∠ACP (Given)
Hence, △ABP ≅ △ACP by SAS axiom.
∠PAB = ∠PAC (Corresponding angles of congruent triangles are equal.)
Thus AP, bisects ∠BAC.
Hence, proved that AP bisects ∠BAC.
Related Questions
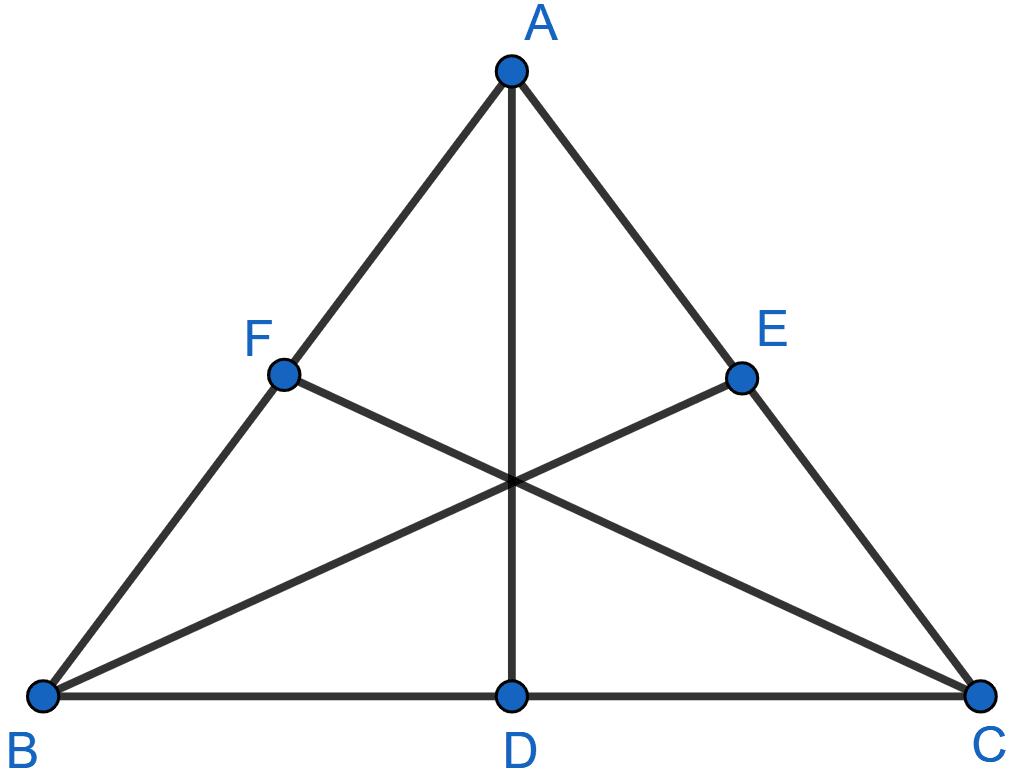
In the adjoining figure, AD, BE and CF are altitudes of △ABC. If AD = BE = CF, prove that ABC is an equilateral triangle.
In the adjoining figure, D and E are points on the side BC of △ABC such that BD = EC and AD = AE. Show that △ABD ≅ △ACE.

In a triangle ABC, AB = AC, D and E are points on the sides AB and AC respectively such that BD = CE. Show that:
(i) △DBC ≅ △ECB
(ii) ∠DCB = ∠EBC
(iii) OB = OC, where O is the point of intersection of BE and CD.
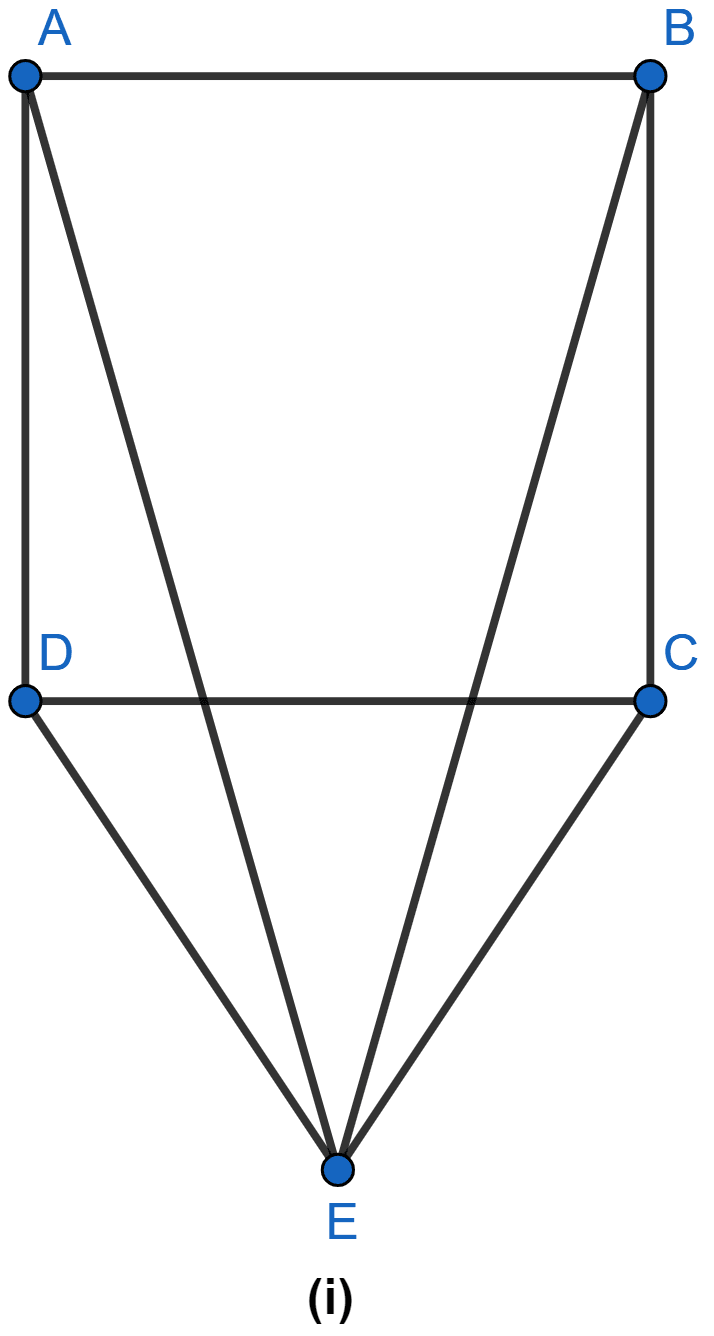
In the figure (i) given below, CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that △ADE ≅ △BCE and hence, AEB is an isosceles triangle.