Mathematics
ABC is a triangle. In order to draw a tangent PQ to the circle at point A, the angle BAQ is drawn equal to :
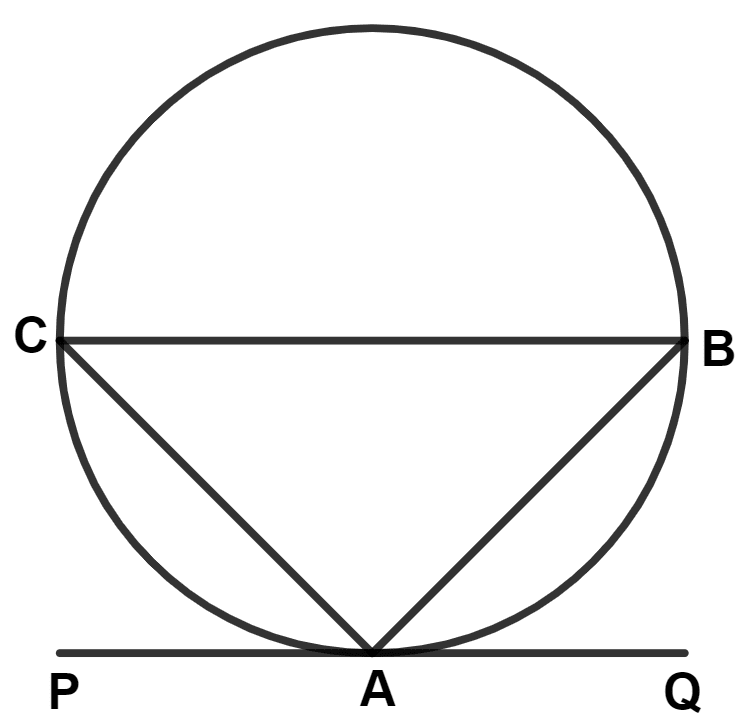
∠BAC
∠BCA
∠ABC
∠PAC
Constructions
3 Likes
Answer
We know that,
The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.
∴ ∠BAQ = ∠BCA.
Hence, Option 2 is the correct option.
Answered By
2 Likes
Related Questions
Using a ruler and a compass, construct a triangle ABC in which AB = 7 cm, ∠CAB = 60° and AC = 5 cm. Construct the locus of :
(i) points equidistant from AB and AC.
(ii) points equidistant from BA and BC.
Hence construct a circle touching the three sides of the triangle internally.
Construct a triangle ABC in which AB = 5 cm, BC = 6.8 cm and median AD = 4.4 cm. Draw incircle of this triangle.
Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
In triangle ABC, ∠ABC = 90°, side AB = 6 cm, side BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.