Mathematics
ABC is a triangle as shown in the figure below.
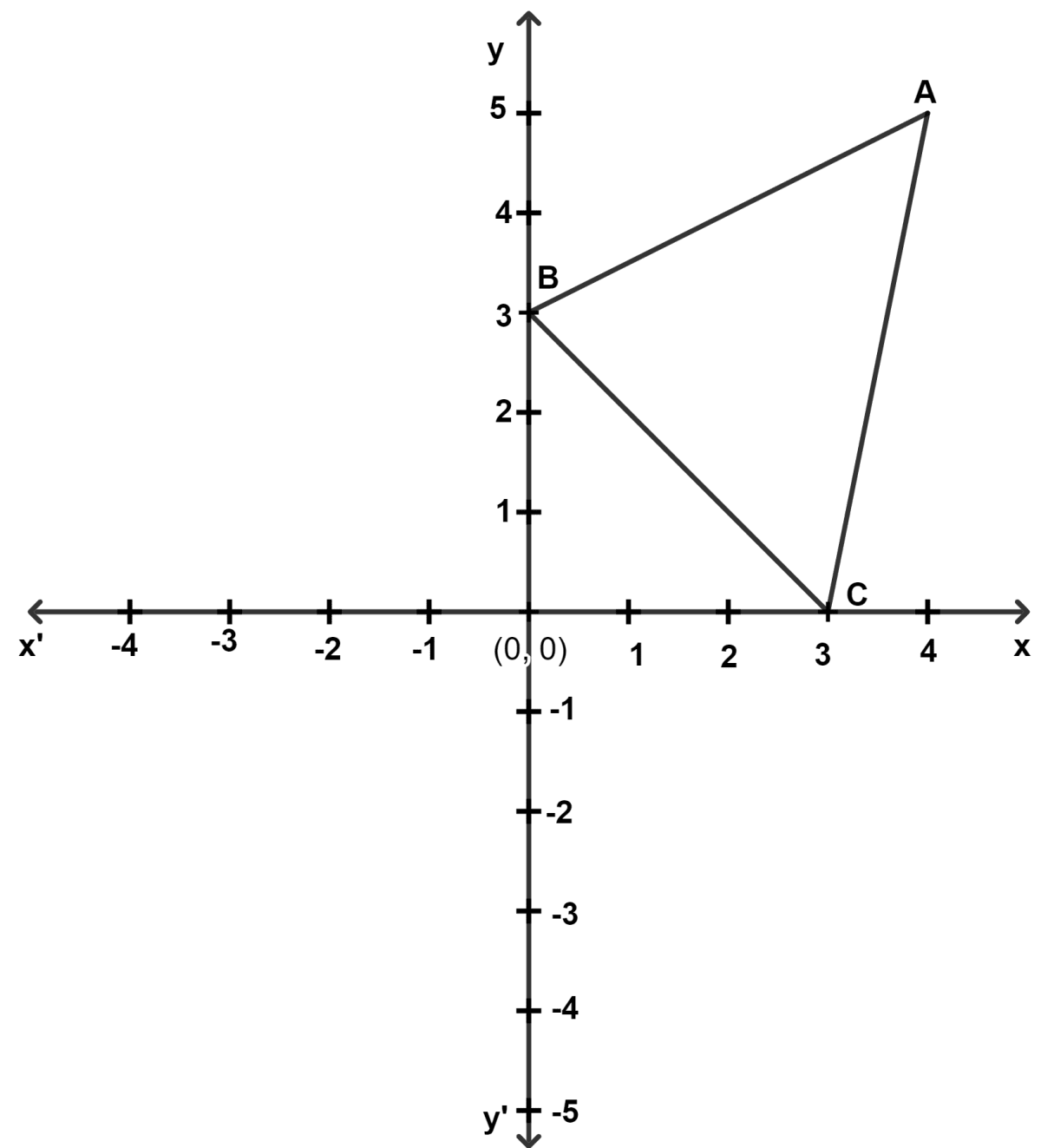
(a) Write down the coordinates of A, B and C on reflecting through the origin.
(b) Write down the coordinates of the point/s which remain invariant on reflecting the triangle ABC on the x-axis and y-axis respectively.
Answer
(a) From figure,
On reflecting in origin A, B and C becomes A', B' and C'.
Coordinates of A' = (-4, -5), B' = (0, -3) and C' = (-3, 0).
Hence, on reflecting A, B and C in origin the coordinates are (-4, -5), (0, -3) and (-3, 0) respectively.
(b) Point C(3, 0) lies on x-axis.
∴ It remains invariant on reflecting in x-axis.
Point B(0, 3) lies on y-axis.
∴ It remains invariant on reflecting in y-axis.
Hence, the invariant point for x-axis is point C and for y-axis is point B.
Related Questions
Square ABCD lies in the third quadrant of a XY plane such that its vertex A is at (-3, -1) and the diagonal DB produced is equally inclined to both the axes. The diagonals AC and BD meets at P(-2, -2). Find the :
(a) Slope of BD
(b) equation of AC
(a) Write the nth term (Tn) of an Arithmetic Progression (A.P.) consisting of all whole numbers which are divisible by 3 and 7.
(b) How many of these are two-digit numbers? Write them.
(c) Find the sum of first 10 terms of this A.P.
Determine the ratio in which the line y = 2 + 3x divides the line segment AB joining the points A(-3, 9) and B(4, 2).