Mathematics
(a) Write the nth term (Tn) of an Arithmetic Progression (A.P.) consisting of all whole numbers which are divisible by 3 and 7.
(b) How many of these are two-digit numbers? Write them.
(c) Find the sum of first 10 terms of this A.P.
AP GP
60 Likes
Answer
(a) A.P. = 21, 42, 63, ………
The above sequence is an A.P. with first term (a) = 21 and common difference (d) = 21.
By formula,
Tn = a + (n - 1)d
= 21 + (n - 1)21
= 21 + 21n - 21
= 21n.
Hence, the nth term = 21n.
(b) A.P. = 21, 42, 63, 84, 105, ……..
Hence, there are four two digit numbers i.e. 21, 42, 63, 84 in the A.P.
(c) By formula,
Sum of A.P. =
Hence, sum of first 10 terms of the A.P. = 1155.
Answered By
28 Likes
Related Questions
Pamela factorized the following polynomial :
2x3 + 3x2 - 3x - 2
She found the result as (x + 2)(x - 1)(x - 2). Using remainder and factor theorem, verify whether her result is correct. If incorrect, give the correct result.
}[r] -6 & 0 \ 4 & 2 \end{bmatrix} \text{ and } B = \begin{bmatrix}[r] 1 & 0 \ 1 & 3 \end{bmatrix}.
Find matrix M, if M = , where l is the identity matrix.
Write the first five terms of the sequence given by , n ∈ N.
(a) Is the sequence an A.P. or G.P.?
(b) If the sum of its first ten terms is , find the value of p.
ABC is a triangle as shown in the figure below.
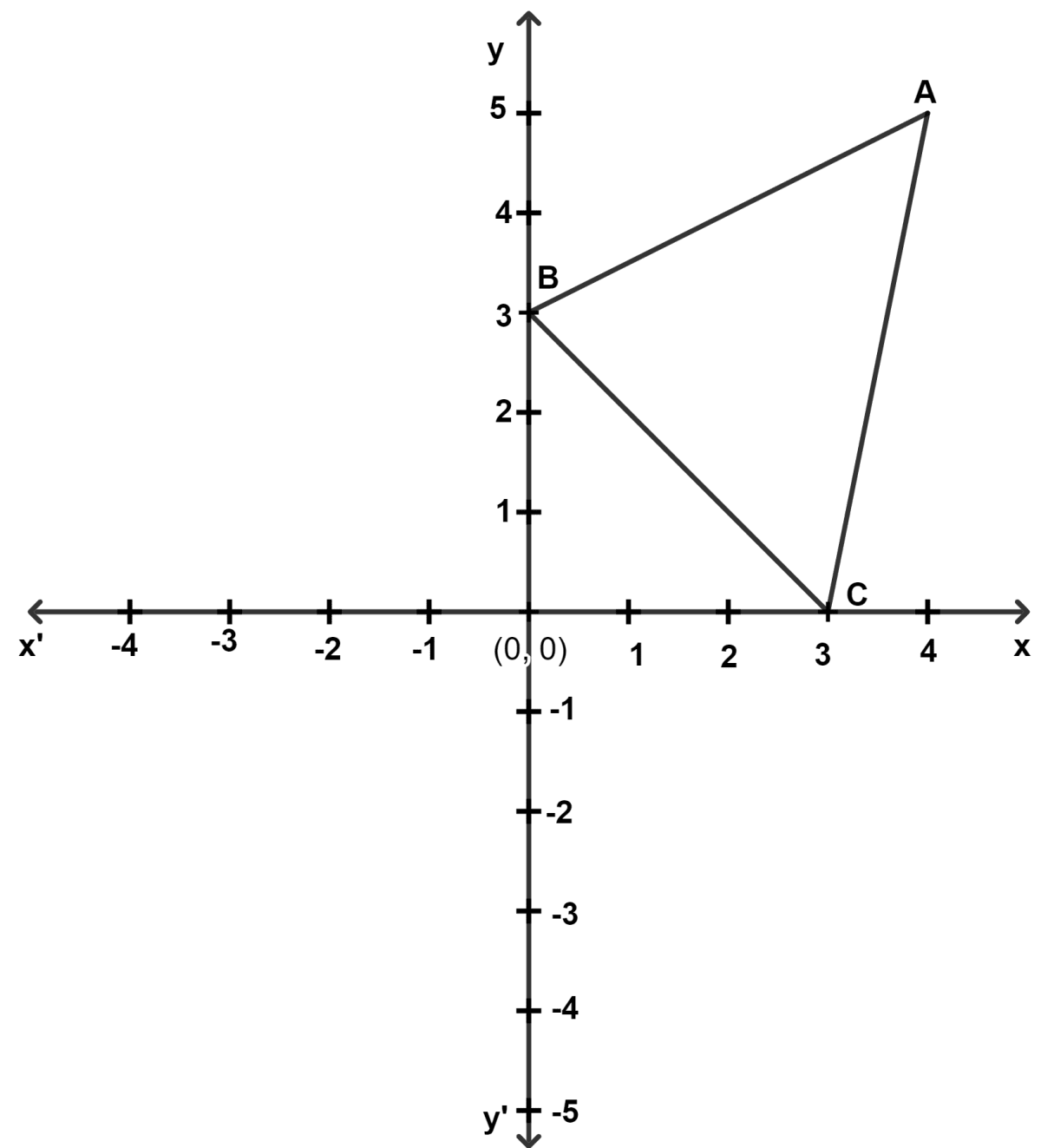
(a) Write down the coordinates of A, B and C on reflecting through the origin.
(b) Write down the coordinates of the point/s which remain invariant on reflecting the triangle ABC on the x-axis and y-axis respectively.