Mathematics
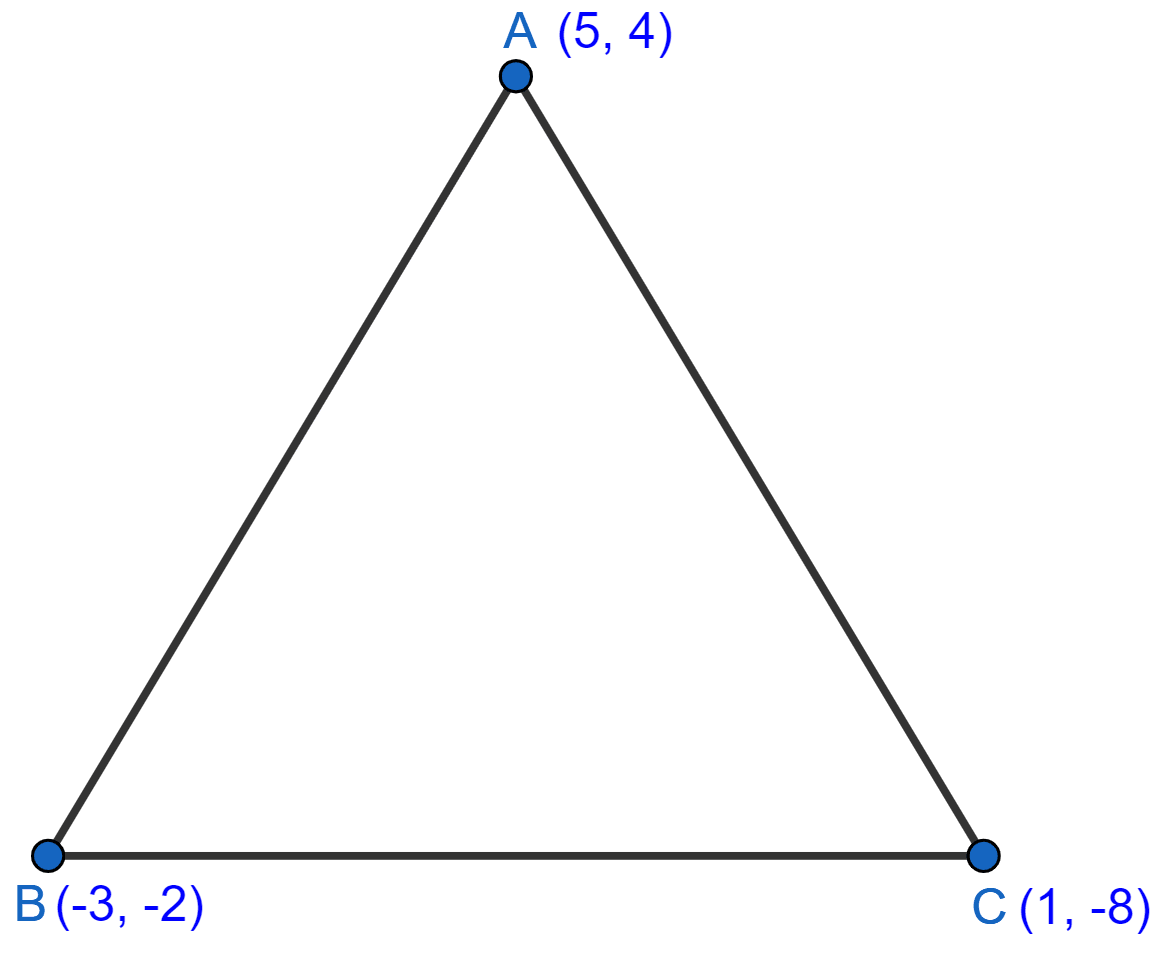
A(5, 4), B(-3, -2) and C(1, -8) are the vertices of a triangle ABC. Find :
(i) the slope of the altitude of AB,
(ii) the slope of the median AD and
(iii) the slope of the line parallel to AC.
Straight Line Eq
19 Likes
Answer
(i) By formula,
Slope =
We know that,
Product of slope of perpendicular lines = -1.
∴ Slope of AB × Slope of altitude = -1
⇒ x Slope of altitude = -1
⇒ Slope of altitude =
Hence, slope of the altitude of AB = .
(ii) Since, AD is median. So, D is the mid-point of BC.
D =
Hence, slope of the median AD = .
(iii)
Since, slope of parallel lines are equal.
Hence, slope of line parallel to AC = 3.
Answered By
9 Likes
Related Questions
Show that the points P(a, b + c), Q(b, c + a) and R(c, a + b) are collinear.
Find x, if the slope of the line joining (x, 2) and (8, -11) is .
The slope of the side BC of a rectangle ABCD is . Find :
(i) the slope of the side AB,
(ii) the slope of the side AD.
The points (K, 3), (2, -4) and (-K + 1, -2) are collinear. Find K.