KnowledgeBoat Logo

Computer Applications

A trigonometrical expression is given as:
(Tan A - Tan B) / (1 + Tan A * Tan B)

Write a program to calculate the value of the given expression by taking the values of angles A and B (in degrees) as input.

Hint: radian= (22 / (7 * 180)) * degree

Java

Java Math Lib Methods

36 Likes

Answer

import java.util.Scanner;

public class KboatTrigExp
{
    public static void main(String args[]) {
        
        Scanner in = new Scanner(System.in);
        
        System.out.print("Enter angle A in degrees: ");
        double angleADeg = in.nextDouble();
        
        System.out.print("Enter angle B in degrees: ");
        double angleBDeg = in.nextDouble();
        
        double angleARad = (22 * angleADeg) / (7 * 180);
        double angleBRad = (22 * angleBDeg) / (7 * 180);
        
        double numerator = Math.tan(angleARad) - Math.tan(angleBRad);
        double demoninator = 1 + Math.tan(angleARad) * Math.tan(angleBRad);
        double trigExp = numerator / demoninator;
        
        System.out.println("tan(A - B) = " + trigExp);
    }
}

Variable Description Table

Program Explanation

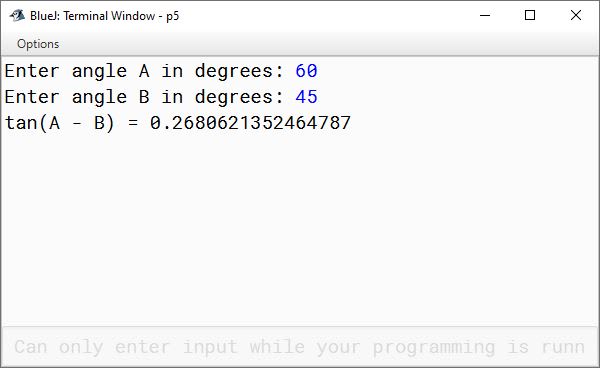
Output

BlueJ output of A trigonometrical expression is given as: (Tan A - Tan B) / (1 + Tan A * Tan B) Write a program to calculate the value of the given expression by taking the values of angles A and B (in degrees) as input. Hint: radian= (22 / (7 * 180)) * degree

Answered By

13 Likes

Related Questions