Mathematics
A straight line passes through the points P(-1, 4) and Q(5, -2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find :
(i) the equation of the line.
(ii) the co-ordinates of points A and B.
(iii) the co-ordinates of point M.
Straight Line Eq
5 Likes
Answer
(i) Slope of PQ = = -1.
By point-slope form,
Equation of PQ is :
⇒ y - y1 = m(x - x1)
⇒ y - 4 = -1[x - (-1)]
⇒ y - 4 = -1(x + 1)
⇒ y - 4 = -x - 1
⇒ x + y = -1 + 4
⇒ x + y = 3.
Hence, the equation of the line is x + y = 3.
(ii) Given,
PQ intersects x-axis at A and y-axis at B.
At x-axis, y co-ordinate = 0.
Substituting y = 0 in equation we get,
⇒ x + 0 = 3
⇒ x = 3.
∴ A = (3, 0)
At y-axis, x co-ordinate = 0.
Substituting x = 0 in equation we get,
⇒ 0 + y = 3
⇒ y = 3.
∴ B = (0, 3)
Hence, co-ordinates of A = (3, 0) and B = (0, 3).
(iii) By formula,
Mid-point =
Substituting values we get,
Hence, co-ordinates of M = .
Answered By
4 Likes
Related Questions
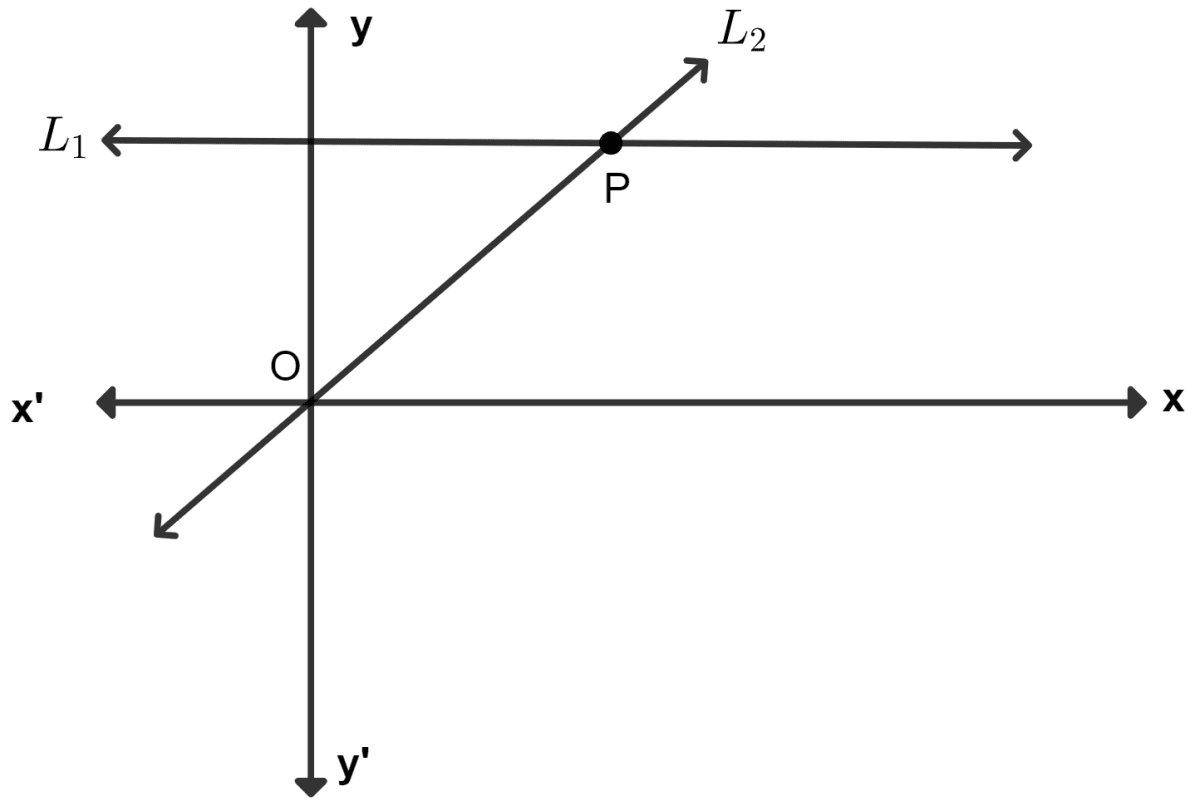
Given equation of line L1 is y = 4.
(i) Write the slope of line L2 if L2 is the bisector of angle O.
(ii) Write the co-ordinates of point P.
(iii) Find the equation of L2.
Find the equation of the line that has x-intercept = -3 and is perpendicular to 3x + 5y = 1.
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find :
(i) equation of line AB.
(ii) equation of line CD.
(iii) co-ordinates of point E and D.

Find the equation of the line through the points A(-1, 3) and B(0, 2). Hence, show that the points A, B and C(1, 1) are collinear.