Physics
A simple U tube contains mercury to the same level in both of it's arms. If water is poured to a height of 13.6 cm in one arm, how much will be the rise in mercury level in the other arm ?
Given: density of mercury = 13.6 x 103 kg m-3 and density of water = 103 kg m-3
Fluids Pressure
111 Likes
Answer
Given,
ρm = 13.6 x 103 kg m -3
ρw = 103 kg m -3
Height to which water is poured in one arm, hw = 13.6 cm
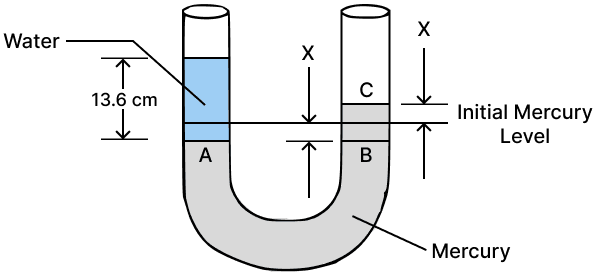
By pouring 13.6 cm of water, the mercury level in the left arm goes down to point A by x cm, while in the right arm, it rises to point C by x cm. Therefore, BC = hm = 2x cm
By Pascal's law,
Pressure in the water column = pressure in the mercury column
Therefore, PA = PB
⇒ hw ρw g = hm ρm g
⇒ 13.6 x 103 x g = 2𝑥 x 13.6 x 103 x g
⇒ 1 = 2𝑥
⇒ 𝑥 = 1/2 = 0.5 cm
Hence, the rise in mercury level = 0.5 cm
Answered By
78 Likes
Related Questions
(a) Calculate the height of a water column which will exert on it's base the same pressure as the 70 cm column of mercury. Density of mercury is 13.6 g cm-3.
(b) Will the height of the water column in part (a) change if the cross section of the water column is made wider ?
The pressure of water on the ground floor is 40,000 Pa and on the first floor is 10,000 Pa. Find the height of the first floor.
(Take : density of water = 1000 kg m-3, g = 10 m s-2)In a hydraulic machine, a force of 2 N is applied on the piston of area of cross section 10 cm 2. What force is obtained on it's piston of area of cross section 100 cm 2?
What should be the ratio of area of cross section of the master cylinder and wheel cylinder of a hydraulic brake so that a force of 15 N can be obtained at each of it's brake shoe by exerting a force of 0.5 N on the pedal ?