Mathematics
A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk of uniform width. Given that the area of the walk is 120 square metres, assuming the width of the walk to be x, form an equation in x and solve it to find the value of x.
Mensuration
32 Likes
Answer
Let ABCD be a rectangular garden.
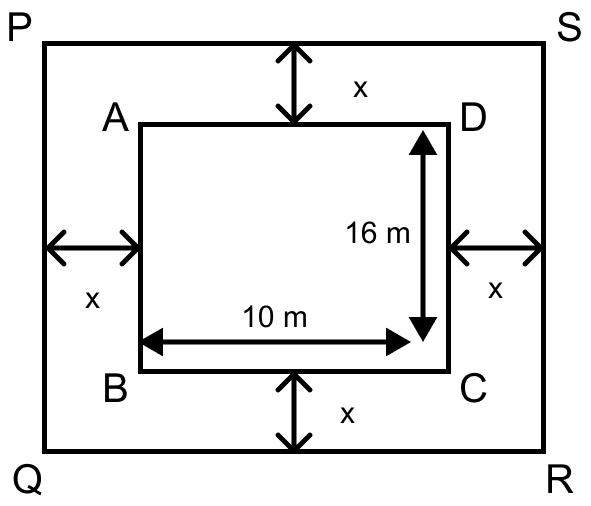
Length = 10 m and Breadth = 16 m.
Area of garden ABCD = l × b
= 10 × 16 = 160 m2
Given, width of the walk = x meters.
From figure,
Length of rectangular garden PQRS = 10 + x + x = (10 + 2x) m
Breadth of rectangular garden PQRS = 16 + x + x = (16 + 2x) m
From figure,
⇒ Area of walk = Area of rectangle PQRS - Area of rectangle ABCD
⇒ 120 = (10 + 2x)(16 + 2x) - 160
⇒ 120 = 160 + 20x + 32x + 4x2 - 160
⇒ 120 = 4x2 + 52x
⇒ 4x2 + 52x - 120 = 0
⇒ 4(x2 + 13x - 30) = 0
⇒ x2 + 13x - 30 = 0
The above equation is the equation in x.
Solving further,
⇒ x2 + 15x - 2x - 30 = 0
⇒ x(x + 15) - 2(x + 15) = 0
⇒ (x - 2)(x + 15) = 0
⇒ x = 2 or x = -15.
Since, length cannot be negative.
∴ x = 2.
Hence, equation is x2 + 13x - 30 = 0 and x = 2 metres.
Answered By
15 Likes
Related Questions
A rectangular floor which measures 15 m × 8 m is to be laid with tiles measuring 50 cm × 25 cm. Find the number of tiles required. Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is uncovered?
The width of a rectangular room is of its length metres. If its perimeter is metres, write an equation connecting and . Find the floor area of the room if its perimeter is 32 m.
A rectangular room is 6 m long, 4.8 m wide and 3.5 m high. Find the inner surface area of the four walls.
A rectangular plot of land measures 41 metres in length and 22.5 metres in width. A boundary wall 2 metres high is built all around the plot at a distance of 1.5 m from the plot. Find the inner surface area of the boundary wall.