A rectangular floor which measures 15 m × 8 m is to be laid with tiles measuring 50 cm × 25 cm. Find the number of tiles required. Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is uncovered?

Let ABCD be the rectangular floor and PQRS be the carpet.

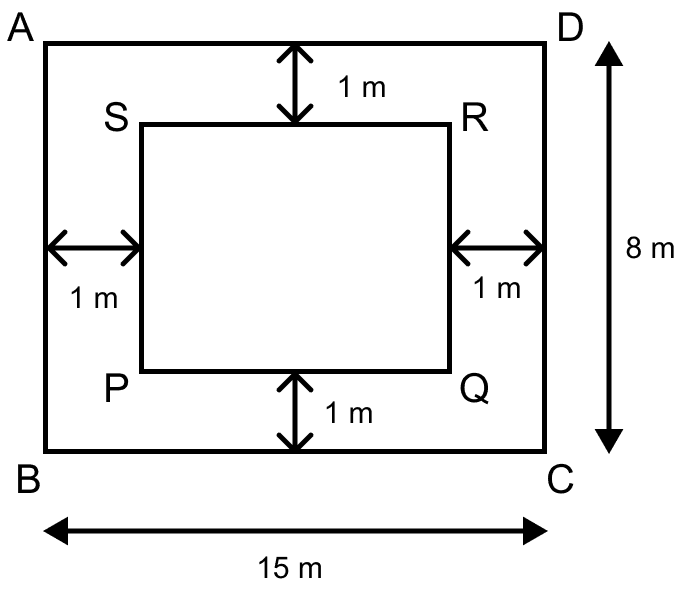
Area of floor = l × b = 15 × 8 = 120 m² = 120 × (100 cm)² = 1200000 cm²

Area of a tile = 50 cm × 25 cm = 1250 cm²

No. of required tiles = $\dfrac{\text{Area of rect. floor}}{\text{Area of a tile}}$

Substituting the values we get,

No. of required tiles = $\dfrac{1200000}{1250}$ = 960.

From figure,

Length of carpet (PQ) = 15 – 1 – 1

= 15 – 2

= 13 m

Breadth of carpet (QR) = 8 – 1 – 1

= 8 – 2

= 6 m

Area of carpet = l × b

= 13 × 6

= 78 m².

Area of floor which is uncovered by carpet = Area of floor – Area of carpet

= 120 – 78

= 42 m²

Fraction of floor uncovered = $\dfrac{\text{Area of floor uncovered}}{\text{Area of floor}}$

= $\dfrac{42}{120} = \dfrac{7}{20}$.

Hence, number of tiles required to cover the floor = 960 tiles and $\dfrac{7}{20}$ is the fraction of floor uncovered.