Mathematics
A rectangle has twice the area of a square. The length of the rectangle is 12 cm greater and the width is 8 cm greater than a side of a square. Find the perimeter of the square.
Answer
Let length of a side of a square = x cm.
According to question,
Length of rectangle = (x + 12) cm
Breadth of rectangle = (x + 8) cm
Given,
⇒ Area of rectangle = 2 × area of square
⇒ (x + 12)(x + 8) = 2 × (x × x)
⇒ x(x + 8) + 12(x + 8) = 2x2
⇒ x2 + 8x + 12x + 96 = 2x2
⇒ x2 – 2x2 + 8x + 12x + 96 = 0
⇒ -x2 + 20x + 96 = 0
⇒ x2 – 20x – 96 = 0
⇒ x2 – 24x + 4x – 96 = 0
⇒ x(x - 24) + 4(x - 24) = 0
⇒ (x + 4)(x – 24) = 0
⇒ x + 4 = 0 or x - 24 = 0
⇒ x = -4 or x = 24 cm
Since, side of a square cannot be negative.
∴ x ≠ -4.
Side of square = 24 cm
Perimeter of square = 4 × side = 4 × 24
= 96 cm.
Hence, perimeter of square = 96 cm.
Related Questions
The perimeter of a square is 48 cm. The area of a rectangle is 4 cm2 less than the area of the square. If the length of the rectangle is 4 cm greater than its breadth, find the perimeter of the rectangle.
The length of a rectangular garden is 12 m more than its breadth. The numerical value of its area is equal to 4 times the numerical value of its perimeter. Find the dimensions of the garden.
If the perimeter of a rectangular plot is 68 m and length of its diagonal is 26 m, find its area.
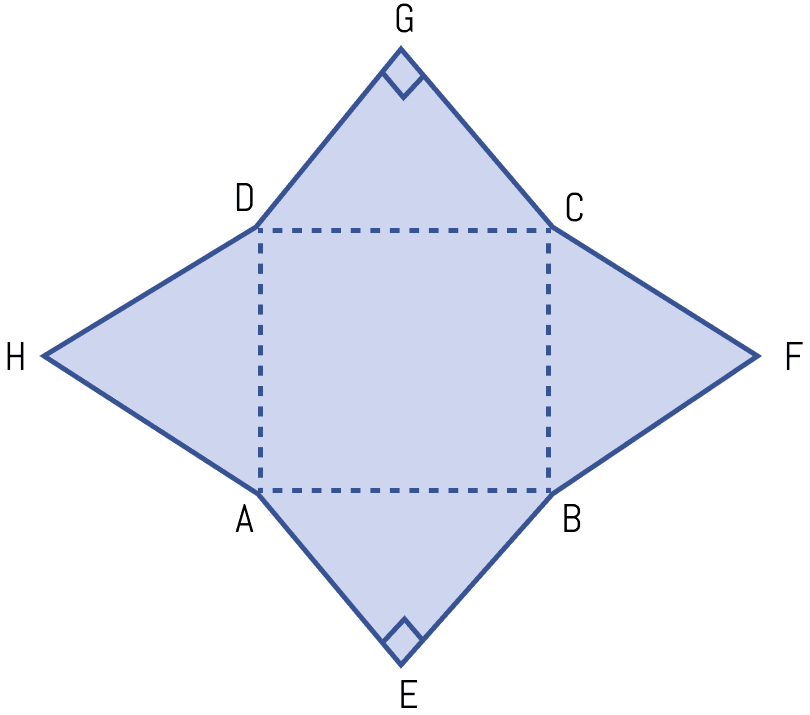
In the adjoining figure, ABCD is a rectangle with sides AB = 10 cm and BC = 8 cm. HAD and BFC are equilateral triangles; AEB and DCG are right angled isosceles triangles. Find the area of the shaded region and the perimeter of the figure.