Physics
A ray of light is normally incident on one face of an equilateral glass prism.
Answer the following —
(a) What is the angle of incidence on the first face of the prism?
(b) What is the angle of refraction from the first face of the prism?
(c) What will be the angle of incidence at the second face of the prism?
(d) Will the light ray suffer minimum deviation by the prism?
Refraction Plane Surfaces
ICSE
68 Likes
Answer
(a) The angle of incidence on the first face of the prism when a ray of light is normally incident is 0°.
(b) The angle of refraction from the first face of the prism r1 = 0° as the angle of refraction of a normally incident ray is always 0°.
(c) As the prism is equilateral therefore A = 60°.
Given, r1 = 0°.
Hence, taking into consideration the two conditions we get,
the angle of incidence at the second face of the prism, equal to 60°.
(d) No, the light ray will not suffer minimum deviation as the angle of incidence is 0°.
Answered By
48 Likes
Related Questions
Draw a ray diagram to show the refraction of a monochromatic ray through a prism when it suffers minimum deviation. How is the angle of emergence related to the angle of incidence in this position.
An object is viewed through a glass prism with its vertex pointing upwards. Draw a ray diagram to show the formation of its image as seen by the observer on the other side of the object.
(a) How does the angle of deviation produced by a prism change with increase in the angle of incidence. Draw a curve showing the variation in the angle of deviation with the angle of incidence at a prism surface.
(b) Using the curve in part (a) above, how would you infer that for a given prism, the angle of minimum deviation 𝛿min is unique for light of a given wavelength.
The diagram below shows two identical prisms A and B placed with their faces parallel to each other. A ray of light of single colour PQ is incident at the face of the prism A. Complete the diagram to show the path of the ray till it emerges out of the prism B.
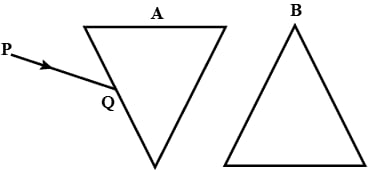
[Hint: The emergent ray out of the prism B will be parallel to the incident ray PQ]