Mathematics
A man on the deck of a ship is 16 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 30°. Calculate the distance of the cliff from the ship and the height of the cliff.
Heights & Distances
39 Likes
Answer
Let A be the man on the deck of the ship B and CE is the cliff.
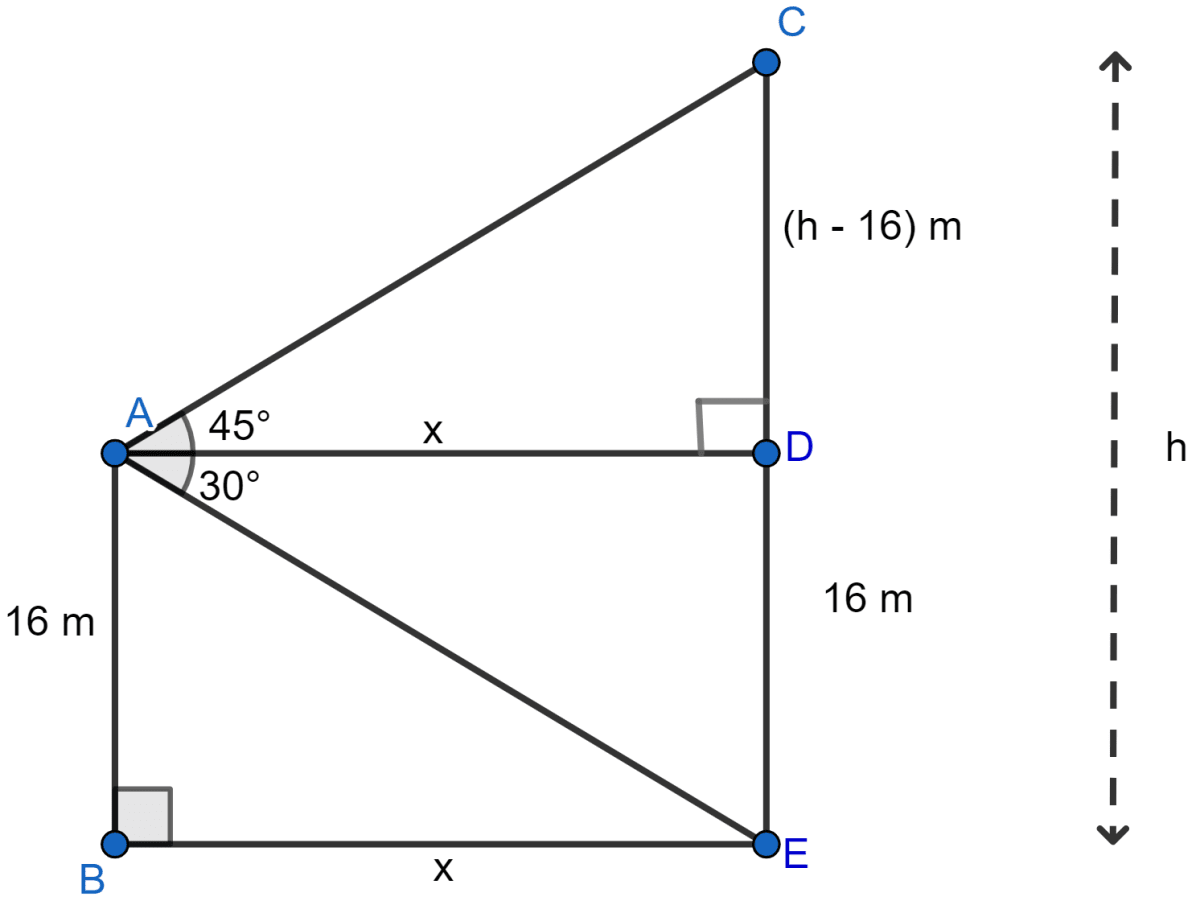
AB = 16 m and angle of elevation of the top of cliff is 45° and angle of depression of base of cliff is 30°.
Let CE = h, AD = x, then
CD = h - 16, AD = BE = x.
Now in right angled triangle △CAD,
Again in right angled triangle △ADE,
From (i) and (ii),
Hence, the distance of cliff from the ship is 27.71 m and height of cliff is 43.71 m.
Answered By
9 Likes
Related Questions
A boy 1.54 m tall can just see the sun over a wall 3.64 m high which is 2.1 m away from him. Find the angle of elevation of the sun.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/h.
There is a small island in between a river 100 meters wide. A tall tree stands on the island. P and Q are points directly opposite to each other on the two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are 30° and 45° respectively, find the height of the tree.
A man standing on the deck of the ship which is 20 m above the sea level, observes the angle of elevation of a bird as 30° and the angle of depression of its reflection in the sea as 60°. Find the height of the bird.