A man observes the angle of elevation of the top of a tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m, the angle of elevation changes to be 60°. Find the height of the tower correct to 2 significant figures.

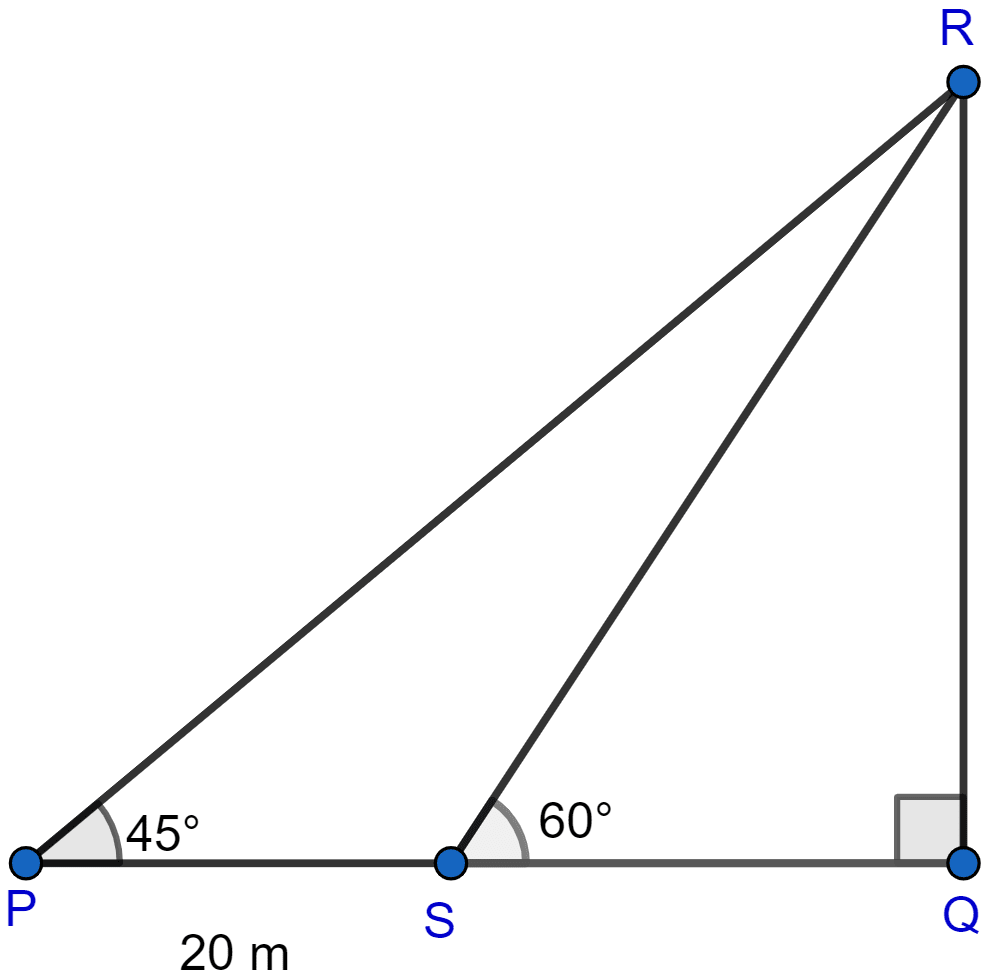
Let tower be QR and initial position of man be P, since the initial angle of elevation is 45°, considering right angled △PQR we get,

$\Rightarrow \text{tan 45°} = \dfrac{QR}{PQ} \\[1em] \Rightarrow 1 = \dfrac{QR}{PQ} \\[1em] \Rightarrow PQ = QR.$

After covering 20 m let the man be at point S, so PS = 20 m and SQ = PQ - PS = PQ - 20 = QR - 20.

Now considering right angled △SQR we get,

$\Rightarrow \text{tan 60°} = \dfrac{QR}{SQ} \\[1em] \Rightarrow \sqrt{3} = \dfrac{QR}{QR - 20} \\[1em] \Rightarrow \sqrt{3}(QR - 20) = QR \\[1em] \Rightarrow \sqrt{3}QR - 20\sqrt{3} = QR \\[1em] \Rightarrow \sqrt{3}QR - QR = 20\sqrt{3}\\[1em] \Rightarrow QR(1.732 - 1) = 20 \times 1.732 \\[1em] \Rightarrow 0.732\text{ QR} = 34.64 \\[1em] \Rightarrow QR = \dfrac{34.64}{0.732} \\[1em] \Rightarrow QR = 47.32$

On correcting to 2 significant figures QR = 47.

Hence, the height of the tower is 47 m.