Mathematics
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
Heights & Distances
Answer
Let QR be the tower and man be initially at point P after moving 60 m let it reach point S.
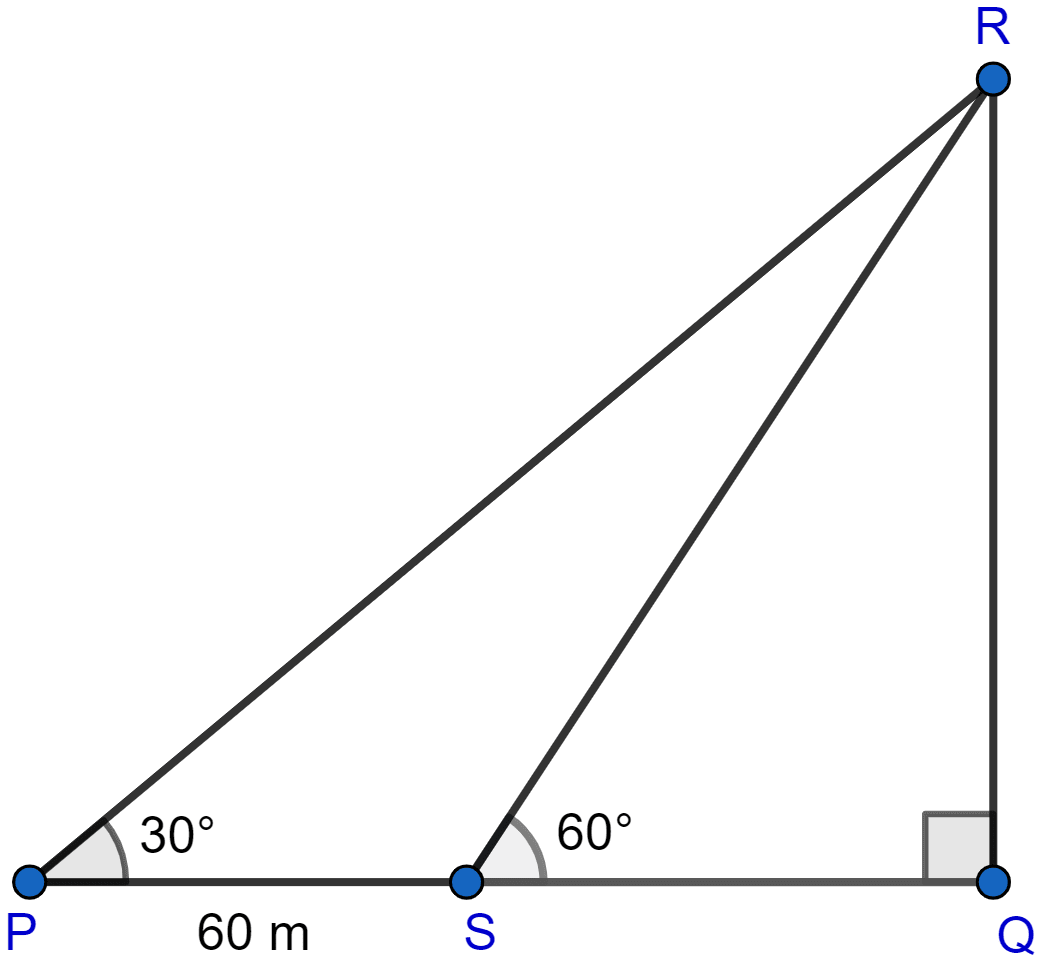
PS = 60 m
From figure,
PQ = PS + SQ = (SQ + 60) m. (Eq 1)
Considering right angled △SQR, we get
Considering right angled △PQR, we get
Putting value of QR from Eq 2, in Eq 3 we get,
From Eq 2,
Correcting upto nearest meter QR = 52.
Hence, the height of building is 52 meters.
Answered By
Related Questions
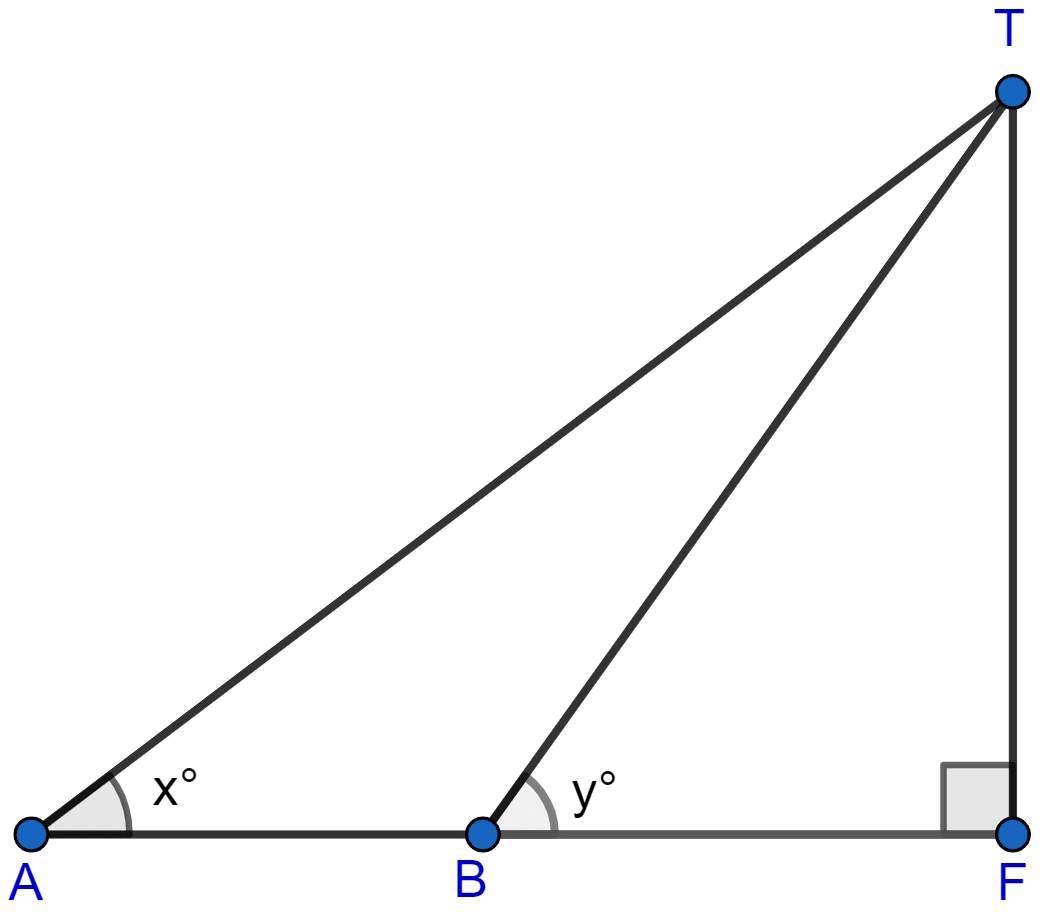
In the figure, not drawn to scale, TF is a tower. The elevation of T from A is x° where tan x = and AF = 200 m. The elevation of T from B, where AB = 80 m, is y°. Calculate :
(i) the height of the tower TF.
(ii) the angle y, correct to the nearest degree.
The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east are found to be 30° and 45° respectively. Find the distance of two stones from the foot of the hill.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is . On walking 192 m towards the tower, the tangent of the angle is found to be . Find the height of the tower.