Mathematics
A hollow cylinder has solid hemisphere inward at one end and on the other end it is closed with a flat circular plate. The height of water is 10 cm when flat circular surface is downward. Find the level of water, when it is inverted upside down, common diameter is 7 cm and height of cylinder is 20 cm.
Mensuration
8 Likes
Answer
Given,
For Cylinder :
Height (H) = 20 cm, Radius (R) = 3.5 cm
For Hemisphere :
Radius (r) = Radius of cylinder (R) = 3.5 cm
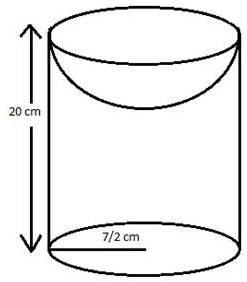
When flat surface is downward, then height of water (h) = 10 cm.
So, when circular surface part will be downward then,
Let height upto which water fills be h1.
Volume of cylinder (upto height h1) = Volume of cylinder (upto height h) + Volume of hemisphere
1 = πR^2h + \dfrac{2}{3}πr^3 \\[1em] \Rightarrow πR^2h1 = πR^2h + \dfrac{2}{3}πR^3 [As, r = R] \\[1em] \Rightarrow πR^2h1 = πR^2\Big(h + \dfrac{2}{3}R\Big) \\[1em] \Rightarrow h1 = h + \dfrac{2}{3}R \\[1em] \Rightarrow h1 = 10 + \dfrac{2}{3}\times 3.5 \\[1em] \Rightarrow h1 = 10 + \dfrac{7}{3} \\[1em] \Rightarrow h1 = \dfrac{30 + 7}{3} \\[1em] \Rightarrow h1 = \dfrac{37}{3} = 12\dfrac{1}{3} = 12.33\text{ cm}.
Hence, the level of water, when cylinder is inverted upside down = 12.33 cm.
Answered By
3 Likes
Related Questions
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is cm and height 8 cm. Find the volume of water required to fill the vessel.
If this cone is replaced by another cone, whose height is cm and the radius of whose base is 2 cm, find the drop in the water level.
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate :
(i) the total surface area of the can in contact with water when the sphere is in it;
(ii) the depth of water in the can before the sphere was put into the can.
The given figure shows a solid cylinder and a solid cone on it according to the given measurement, the total surface area of the solid in terms of π and r is :
4πr2
5πr2
6πr2
7πr2
The radii of two solid spheres are 10 cm and 20 cm. The ratio between their volumes is :
3 : 8
1 : 4
1 : 8
8 : 3
