Mathematics
A foot path of uniform width runs all around the inside of a rectangular field 50 m long and 38 m wide. If the area of the path is 492 m2, find its width.
Answer
Consider ABCD as a rectangular field having, length = 50 m and breadth = 38 m.
Let x meters be the width of foot path.
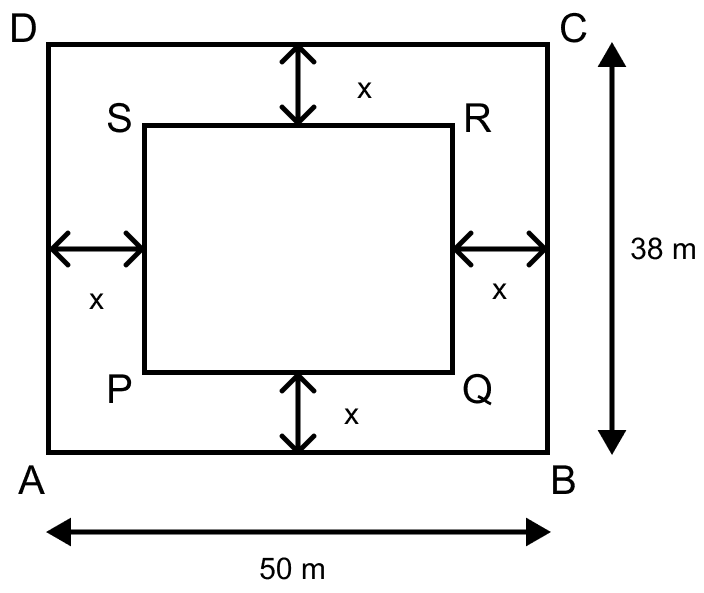
We know that,
Area of rectangular = l × b
From figure,
Area of path = Area of rectangle ABCD - Area of rectangle PQRS
Substituting the values we get,
Area of path = (AB × BC) - (PQ × QR) ……..(1)
From figure,
PQ = AB - x - x = (50 - 2x) m,
QR = BC - x - x = (BC - 2x) m.
Substituting the values in equation 1 we get,
⇒ 492 = (50 × 38) - (50 - 2x) (38 - 2x)
⇒ 492 = 1900 - [50(38 - 2x) - 2x(38 - 2x)]
⇒ 492 = 1900 - (1900 - 100x - 76x + 4x2)
⇒ 492 = 1900 - 1900 + 100x + 76x - 4x2
⇒ 492 = 176x - 4x2
⇒ 492 = 4(44x - x2)
⇒ 123 = 44x - x2
⇒ x2 - 44x + 123 = 0
⇒ x2 - 41x - 3x + 123 = 0
⇒ x(x - 41) - 3(x - 41) = 0
⇒ (x - 3)(x - 41) = 0
⇒ x - 3 = 0 or x - 41 = 0
⇒ x = 3 m or x = 41 m.
Since, width of path cannot be greater than breadth of field,
So, x ≠ 41 m.
Hence, width of the footpath is 3 m.
Related Questions
The shaded region of the given diagram represents the lawn in front of a house. On three sides of the lawn there are flower beds of width 2 m.
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower–beds.

A rectangular plot 20 m long and 14 m wide is to be covered with grass leaving 2 m all around. Find the area to be laid with grass.
A rectangular floor which measures 15 m × 8 m is to be laid with tiles measuring 50 cm × 25 cm. Find the number of tiles required. Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is uncovered?
The cost of enclosing a rectangular garden with a fence all around at the rate of ₹15 per metre is ₹5400. If the length of the garden is 100 m, find the area of the garden.