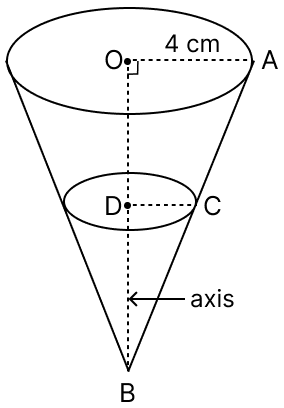
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid-point of its axis and parallel to its base. Compare the volumes of the two parts.

Let height of conical part (BO) be h cm so height of smaller cone (BD) will be $\dfrac{h}{2}$ cm.

In △OBA and △DBC,

∠OBA = ∠DBC (Common)

∠BDC = ∠BOA (Each equal to 90°)

So, △OBA ~ △DBC (By A.A. axiom)

We know that,

Corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{CD}{OA} = \dfrac{BD}{BO} \\[1em] \Rightarrow \dfrac{CD}{4} = \dfrac{\dfrac{h}{2}}{h} \\[1em] \Rightarrow \dfrac{CD}{4} = \dfrac{1}{2} \\[1em] \Rightarrow CD = \dfrac{4}{2} = 2 \text{ cm}.$

By formula,

Volume of cone (V) = $\dfrac{1}{3}πr^2h$

Substituting values we get :

$\Rightarrow V = \dfrac{1}{3}π(4)^2h \\[1em] \Rightarrow V = \dfrac{16}{3}πh.$

Let volume of smaller cone be v. It's height will be $\dfrac{h}{2}$

$\Rightarrow v = \dfrac{1}{3}π(CD)^2 \times \dfrac{h}{2} \\[1em] \Rightarrow v = \dfrac{1}{3}π \times 2^2 \times \dfrac{h}{2} \\[1em] \Rightarrow v = \dfrac{1}{3}π \times 2h \\[1em] \Rightarrow v = \dfrac{2}{3}πh.$

Volume of frustum = Volume of bigger cone - Volume of smaller cone

= $\dfrac{16}{3}πh - \dfrac{2}{3}πh$

= $\dfrac{14}{3}πh$.

Ratio = $\dfrac{\text{Volume of frustum}}{\text{Volume of smaller cone}}$

= $\dfrac{\dfrac{14}{3}πh}{\dfrac{2}{3}πh} = \dfrac{14 \times 3}{2 \times 3} = \dfrac{7}{1}$.

Hence, the ratio of volume of frustum to the smaller cone = 7 : 1.