Mathematics
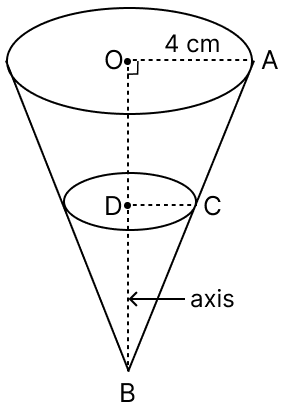
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid-point of its axis and parallel to its base. Compare the volumes of the two parts.
Mensuration
1 Like
Answer
Let height of conical part (BO) be h cm so height of smaller cone (BD) will be cm.
In △OBA and △DBC,
∠OBA = ∠DBC (Common)
∠BDC = ∠BOA (Each equal to 90°)
So, △OBA ~ △DBC (By A.A. axiom)
We know that,
Corresponding sides of similar triangles are proportional.
By formula,
Volume of cone (V) =
Substituting values we get :
Let volume of smaller cone be v. It's height will be
Volume of frustum = Volume of bigger cone - Volume of smaller cone
=
= .
Ratio =
= .
Hence, the ratio of volume of frustum to the smaller cone = 7 : 1.
Answered By
3 Likes
Related Questions
If the mean proportion between x and z is y, find the mean proportion between x2 + y2 and y2 + z2.
Prove that :
.
ABCD is a parallelogram in which vertices B = (5, 8), C = (4, 7) and D = (2, -4). Find :
(i) the coordinates of vertex A.
(ii) the equation of diagonal BD.
On a graph paper plot the triangle ABC whose vertices are at points A(5, 4), B(7, 5) and C(-3, 6). On the same graph, draw the image of the triangle ABC under reflection in the line y = 3. Mark any two points on the graph paper which are invariant under this reflection. Also, write the co-ordinates of points marked.