Mathematics
A bag contains twenty ₹ 5 coins, fifty ₹ 2 coins and thirty ₹ 1 coins. If it is equally likely that one of the coins will fall down when the bag is turned upside down, what is the probability that the coin :
(i) will be a ₹ 1 coin ?
(ii) will not be a ₹ 2 coin ?
(iii) will neither be a ₹ 5 coin nor be a ₹ 1 coin ?
Probability
5 Likes
Answer
We have,
Total number of coins = 20 + 50 + 30 = 100
So, the total possible outcomes = 100.
(i) Number of ₹ 1 coin = 30
∴ Number of favourable outcomes = 30
P(drawing a ₹ 1 coin) = .
Hence, the probability of drawing a ₹ 1 coin = .
(ii) Number of ₹ 5 and ₹ 1 coin = 50 (20 + 30)
Hence, no. of coins apart from ₹ 2 coins = 50.
∴ Number of favourable outcomes = 50
P(coin drawn will not be a ₹ 2 coin) = .
Hence, the probability of not drawing a ₹ 2 coin = .
(iii) No. of ₹ 2 coins = 50
No. of favourable outcomes (for drawing a ₹ 2 coin) = 50
P(drawing a ₹ 2 coin) = .
Since, there are only 3 types of coins in the bag.
∴ P(drawing neither ₹ 5 nor ₹ 1 coin) = P(drawing ₹ 2 coin) = .
Hence, the probability of drawing neither ₹ 5 nor ₹ 1 coin = .
Answered By
4 Likes
Related Questions
A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability that the ball drawn will be :
(i) not red ?
(ii) neither red nor green ?
(iii) white or green ?
The probability that two boys do not have the same birthday is 0.897. What is the probability that the two boys have the same birthday ?
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting :
(i) a queen of red color
(ii) a black face card
(iii) the jack or the queen of the hearts
(iv) a diamond
(v) a diamond or a spade
A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.
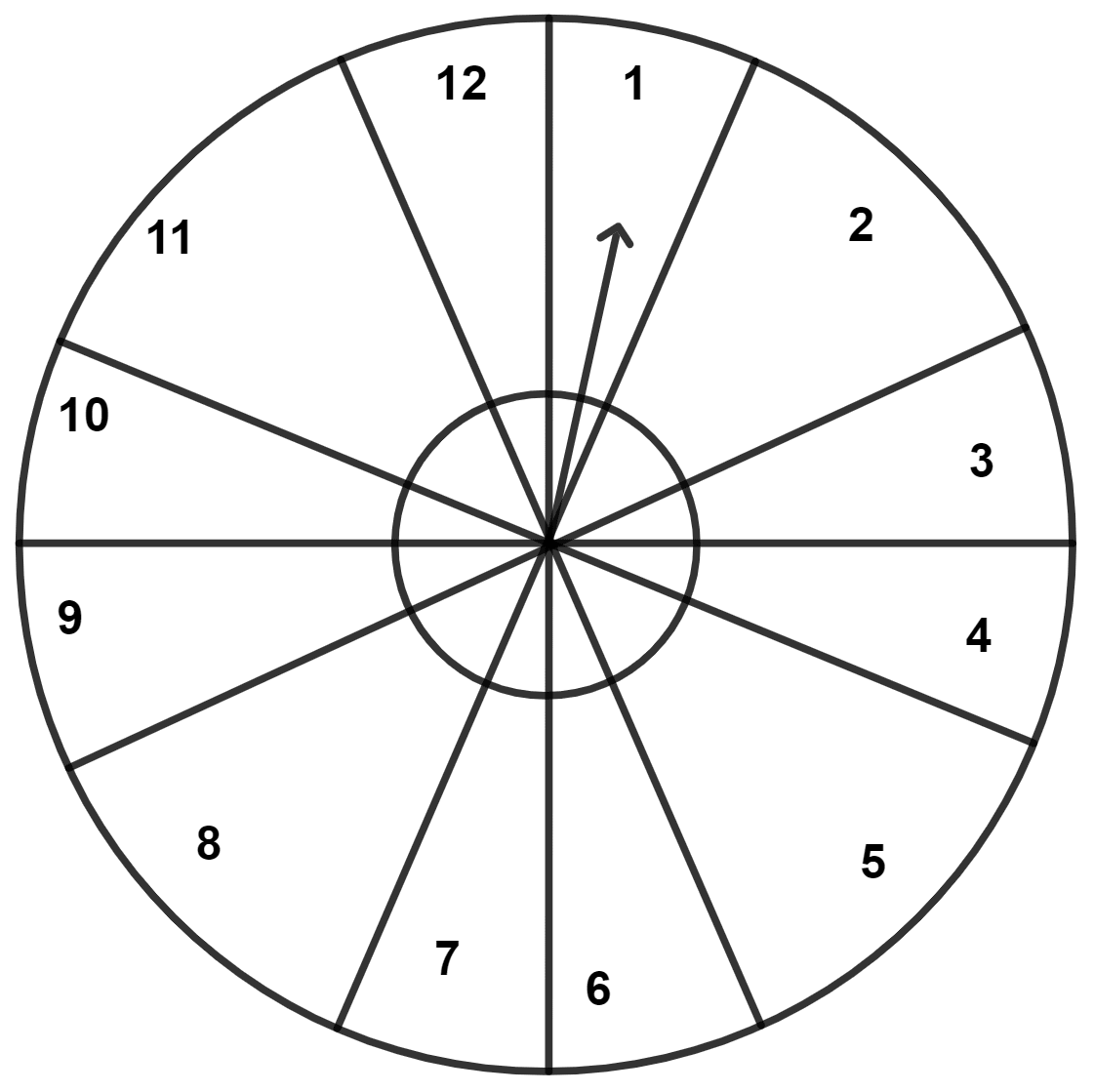
If the outcomes are equally likely, find the probability that the pointer will point at:
(i) 6
(ii) an even number
(iii) a prime number
(iv) a number greater than 8
(v) a number less than or equal to 9
(vi) a number between 3 and 11.