Computer Applications
Write a program to enter a two digit number and find out its first factor excluding 1 (one). The program then find the second factor (when the number is divided by the first factor) and finally displays both the factors.
Hint: Use a non-return type method as void fact(int n) to accept the number.
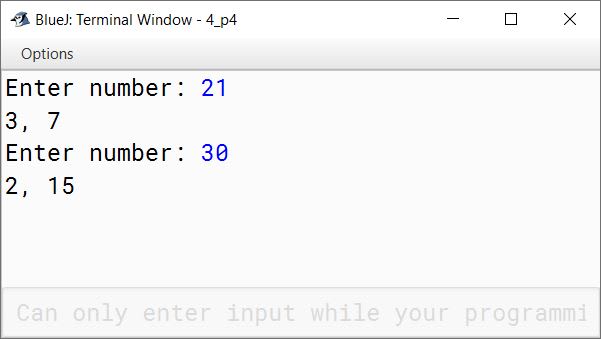
Sample Input: 21
The first factor of 21 is 3
Sample Output: 3, 7
Sample Input: 30
The first factor of 30 is 2
Sample Output: 2, 15
Java
User Defined Methods
64 Likes
Answer
import java.util.Scanner;
public class KboatFactors
{
public void fact(int n) {
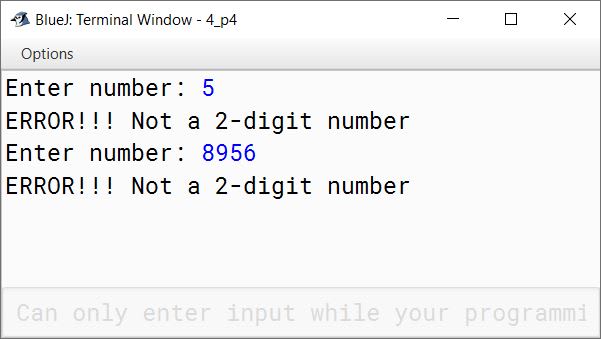
if (n < 10 || n > 99) {
System.out.println("ERROR!!! Not a 2-digit number");
return;
}
int i;
for (i = 2; i <= n; i++) {
if (n % i == 0)
break;
}
int sf = n / i;
System.out.println(i + ", " + sf);
}
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
System.out.print("Enter number: ");
int num = in.nextInt();
KboatFactors obj = new KboatFactors();
obj.fact(num);
}
}Variable Description Table
Program Explanation
Output
Answered By
36 Likes
Related Questions
Write a program to input a three digit number. Use a method int Armstrong(int n) to accept the number. The method returns 1, if the number is Armstrong, otherwise zero(0).
Sample Input: 153
Sample Output: 153 ⇒ 13 + 53 + 33 = 153
It is an Armstrong Number.Write a program to input a number and check and print whether it is a 'Pronic' number or not. Use a method int Pronic(int n) to accept a number. The method returns 1, if the number is 'Pronic', otherwise returns zero (0).
(Hint: Pronic number is the number which is the product of two consecutive integers)Examples:
12 = 3 * 4
20 = 4 * 5
42 = 6 * 7Write a method fact(int n) to find the factorial of a number n. Include a main class to find the value of S where:
S = n! / (m!(n - m)!)
where, n! = 1 x 2 x 3 x ………. x nWrite a program using a method called area() to compute area of the following:
(a) Area of circle = (22/7) * r * r
(b) Area of square= side * side
(c) Area of rectangle = length * breadth
Display the menu to display the area as per the user's choice.