What type of quadrilateral do the points A(2, -2), B(7, 3), C(11, -1) and D(6, -6), taken in that order, form?

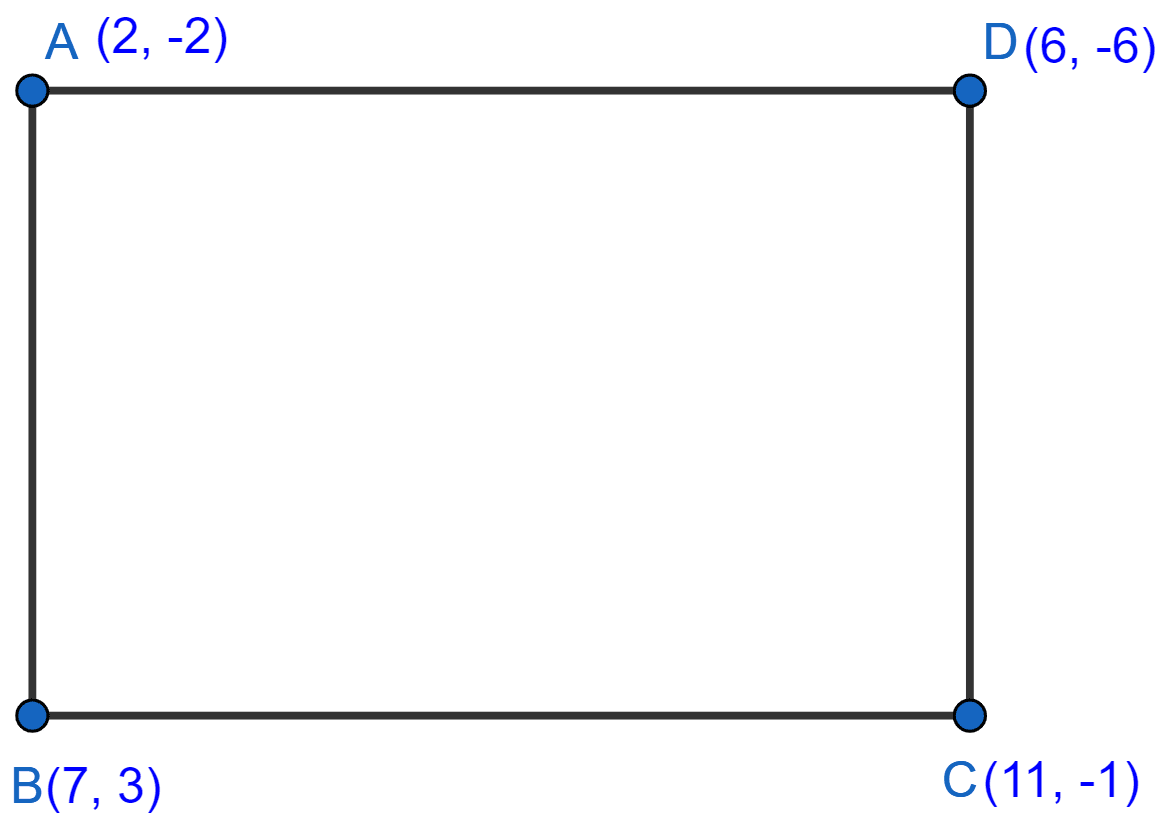
By distance formula,

$d = \sqrt{(x$2 - x1)^2 + (y2 - y1)^2} \\[1em] \therefore AB = \sqrt{(7 - 2)^2 + [3 - (-2)]^2} \\[1em] = \sqrt{5^2 + 5^2} \\[1em] = \sqrt{25 + 25} \\[1em] = \sqrt{50}. \\[1em] \therefore BC = \sqrt{(11 - 7)^2 + (-1 - 3)^2} \\[1em] = \sqrt{4^2 + (-4)^2} \\[1em] = \sqrt{16 + 16} \\[1em] = \sqrt{32}. \\[1em] \therefore CD = \sqrt{(6 - 11)^2 + [-6 - (-1)]^2} \\[1em] = \sqrt{(-5)^2 + (-5)^2} \\[1em] = \sqrt{25 + 25} \\[1em] = \sqrt{50}. \\[1em] \therefore AD = \sqrt{(6 - 2)^2 + [-6 - (-2)]^2} \\[1em] = \sqrt{4^2 + (-4)^2} \\[1em] = \sqrt{16 + 16} \\[1em] = \sqrt{32}.

Hence,

AB = CD and BC = AD

Since, opposite sides are equal,

Hence, proved that ABCD is a rectangle.