Mathematics
Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Triangles
2 Likes
Answer
Let ABC be the triangle, D be the mid-point AB and E be the mid-point of AC.
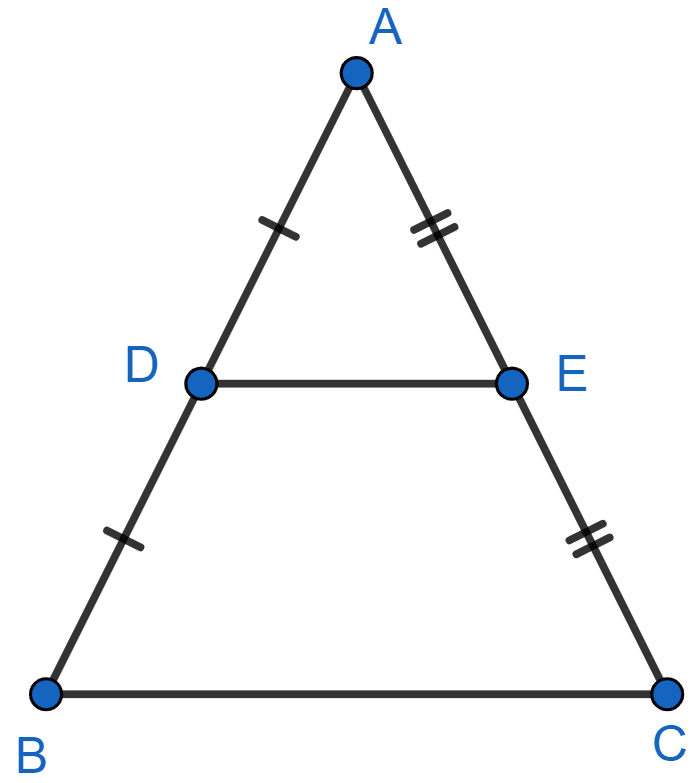
So, in △ ABC,
………(1)
………(2)
From (1) and (2), we get :
.
By theorem 6.2,
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Since, In △ ABC,
.
∴ DE || BC.
Hence, proved that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Answered By
1 Like
Related Questions
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that .
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
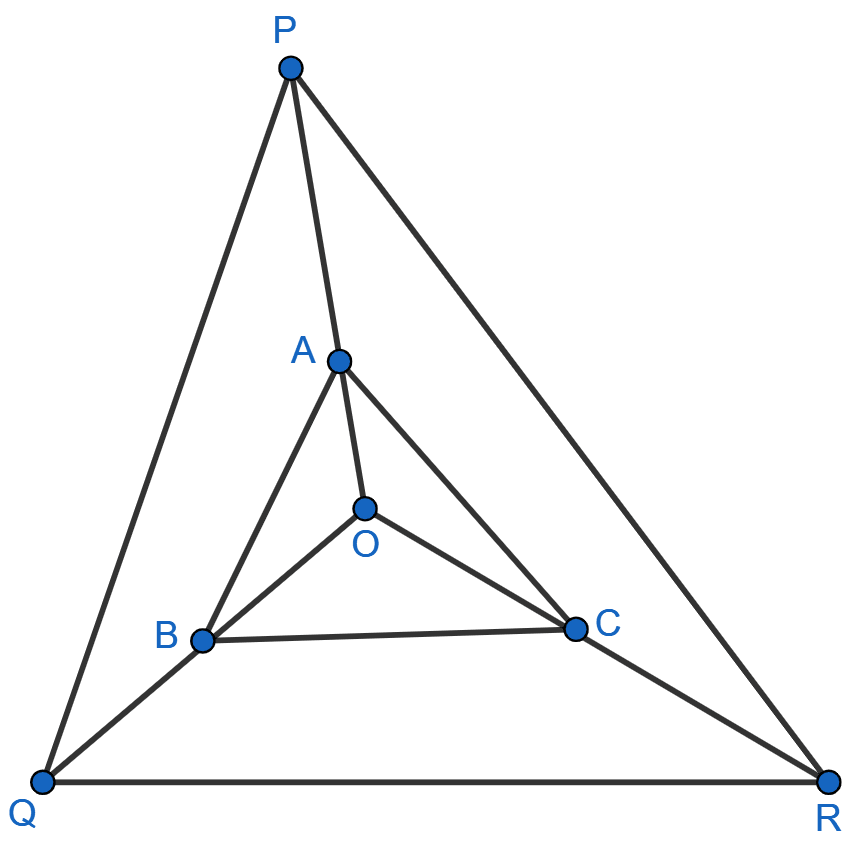
In figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that Show that ABCD is a trapezium.