Mathematics
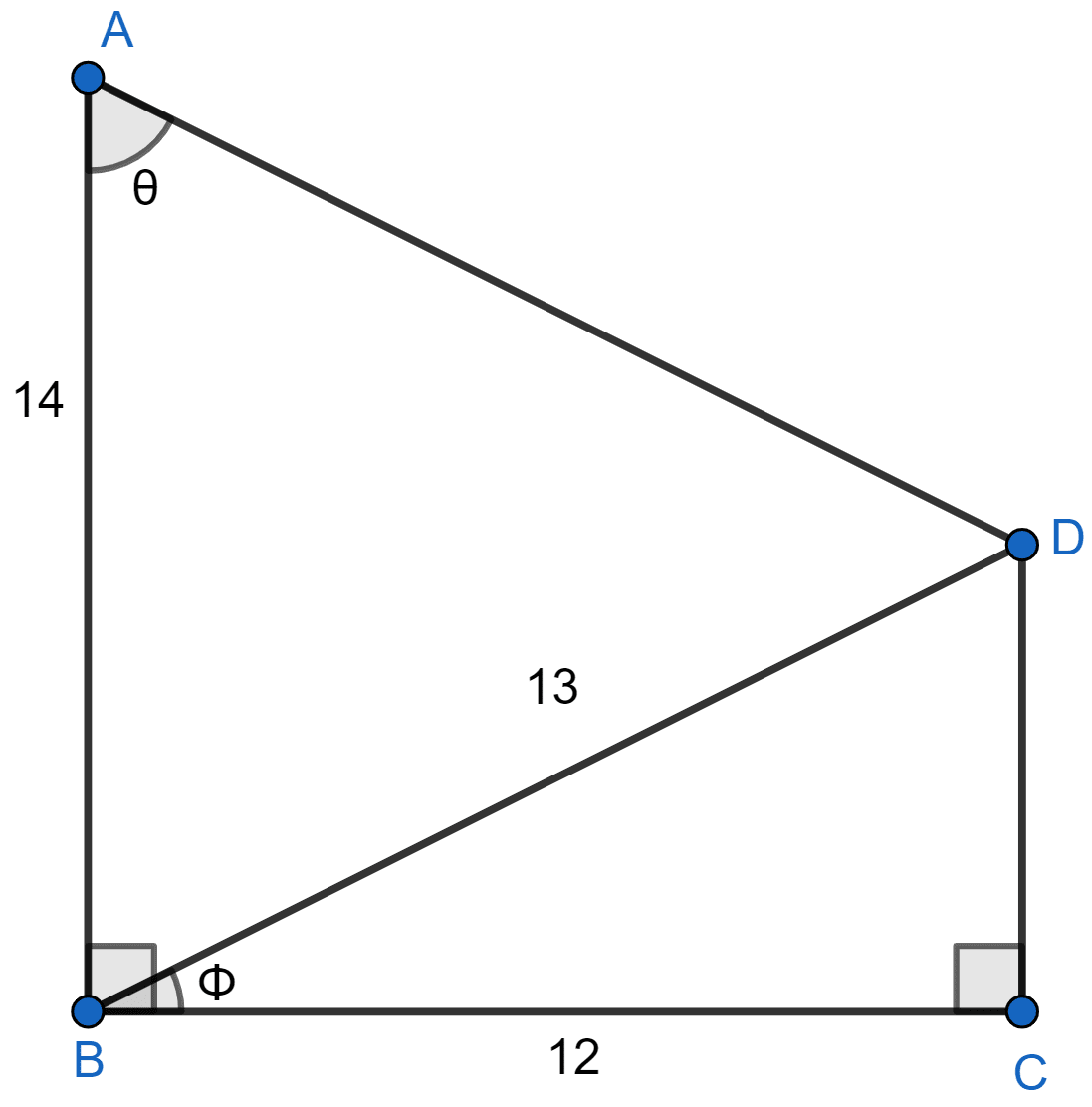
Using the measurements given in the figure alongside,
(a) Find the values of:
(i) sin Φ
(ii) tan θ.
(b) Write an expression for AD in terms of θ.
Trigonometrical Ratios
33 Likes
Answer
(a) In right-angled ∆BCD
Using pythagoras theorem we get :
⇒ BD2 = BC2 + CD2
⇒ CD2 = BD2 - BC2
⇒ CD2 = (13)2 - (12)2
⇒ CD2 = 169 - 144
⇒ CD2 = 25
⇒ CD = = 5.
(i) By formula,
sin Φ =
In right-angled ∆BCD
sin Φ = .
Hence, sin Φ = .
(ii) Draw DE perpendicular to AB.
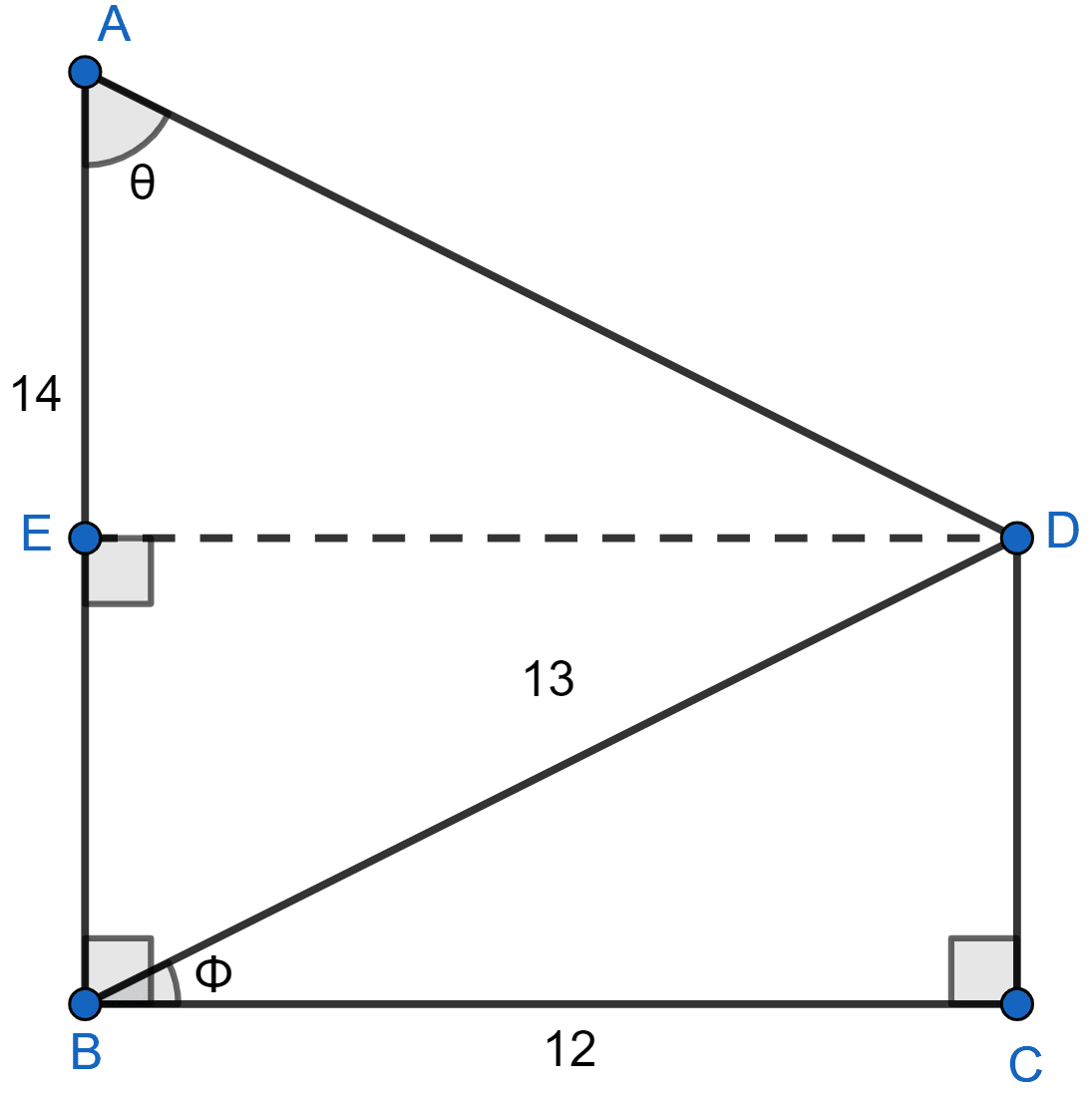
From figure,
ED = BC = 12
In right-angled ∆BED
Using pythagoras theorem we get :
⇒ BD2 = ED2 + EB2
⇒ 132 = 122 + EB2
⇒ EB2 = (13)2 - (12)2
⇒ EB2 = 169 - 144
⇒ EB2 = 25
⇒ EB = = 5.
From figure,
AE = AB - EB = 14 - 5 = 9.
By formula,
tan θ = .
Hence, tan θ = .
(b) In right-angled ∆AED
Hence, AD = .
Answered By
21 Likes
Related Questions
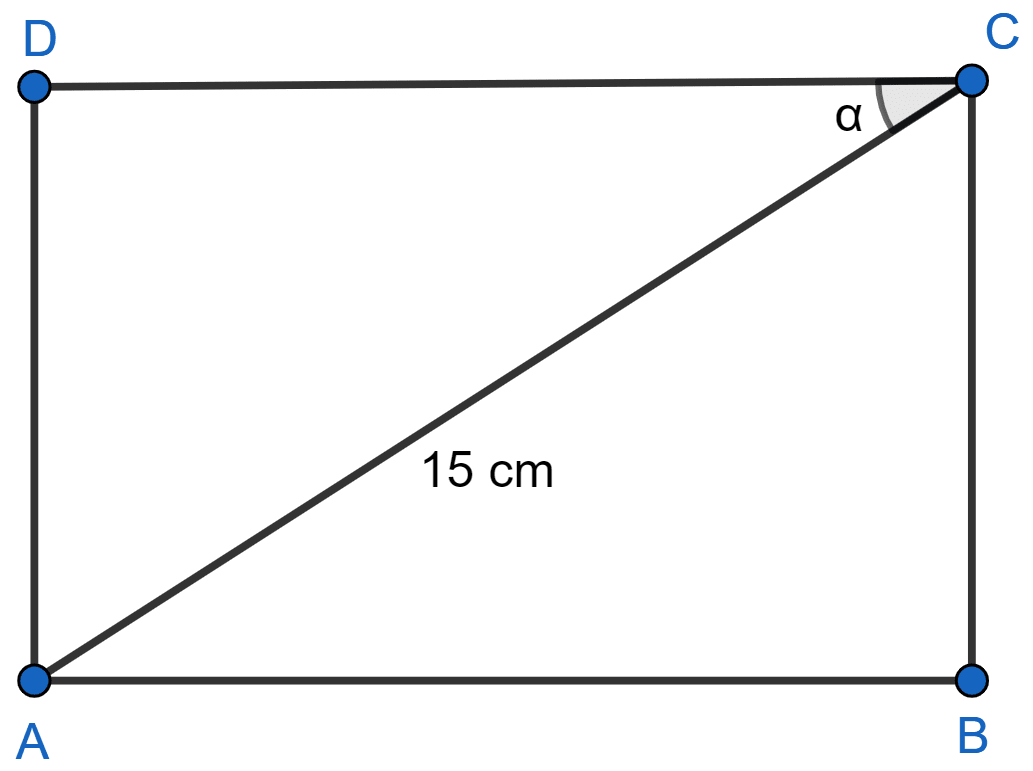
In the adjoining figure, ABCD is a rectangle. Its diagonal AC = 15 cm and ∠ACD = α. If cot α = , find the perimeter and the area of the rectangle.
In the figure (2) given below, ∆ABC is right-angled at B and BD is perpendicular to AC. Find :
(i) cos ∠CBD
(ii) cot ∠ABD

Prove the following:
cot2 A - + 1 = 0
Prove the following:
(sin A + cos A)2 + (sin A - cos A)2 = 2