Mathematics
Using ruler and compasses only,
(i) Construct a triangle ABC with the following data :
Base AB = 6 cm, BC = 7.5 cm and angle CAB = 60°.
(ii) In same diagram, draw a circle which passes through the points A, B and C and mark its center O.
(iii) Draw a perpendicular from O to AB which meets AB in D.
(iv) Prove that : AD = BD.
Answer
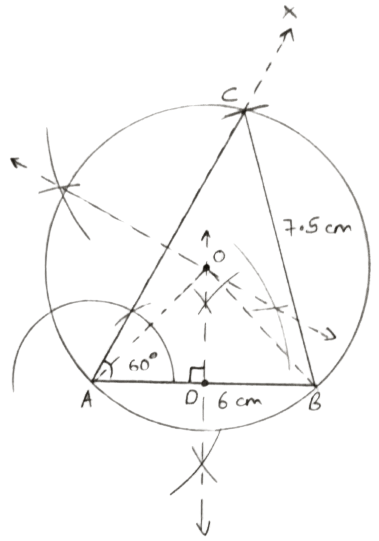
Steps of construction :
Draw a line segment AB = 6 cm.
At A, draw a ray (AX) making an angle of 60° with AB.
With B as center and radius = 7.5 cm draw an arc which intersects AX ray at C.
Join BC. ABC is the required triangle.
Draw the perpendicular bisectors of AB and AC intersecting each other at O.
With center O and radius OA, OB or OC, draw a circle passing through A, B and C.
From O, draw OD ⊥ AB.
Proof :
In right △OAD and △OBD,
⇒ OA = OB (Radius of same circle)
⇒ OD = OD (Common)
⇒ ∠ODA = ∠ODB (Both = 90°)
∴ △OAD ≅ △OBD (By R.H.S. axiom)
By C.P.C.T.
⇒ AD = BD.
Hence, proved that AD = BD.
Related Questions
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Using ruler and compasses only,
(i) Construct triangle ABC, having given BC = 7 cm, AB - AC = 1 cm and ∠ABC = 45°.
(ii) Inscribe a circle in the △ABC constructed in (i) above.
Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
(i) What do you call the point O ?
(ii) What is the relation between the distances OA, OB and OC ?
(iii) Does the perpendicular bisector of BC pass through O ?