Mathematics
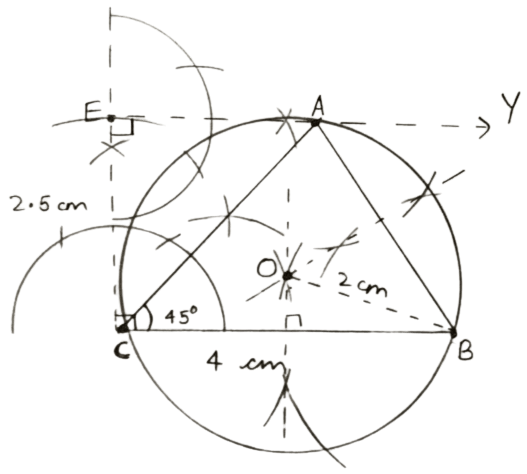
Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC.
Answer
Steps of construction :
Draw a line segment BC = 4 cm.
At C, draw a perpendicular line CX and from it, cut off CE = 2.5 cm.
From E, draw EY, perpendicular to CX.
From C, draw a ray making an angle 45° with CB, which intersects EY at A.
Join AB. Hence, ABC is the required triangle.
Draw perpendicular bisectors of sides AB and BC intersecting each other at O.
With center O, and radius OA or OB or OC draw a circle passing through A, B and C. Measure OB.
On measuring,
OB = 2 cm.
Hence, above is the required circumcircle of △ABC with radius = 2 cm.
Related Questions
The bisectors of angles A and B of a scalene triangle ABC meet at O.
(i) What is the point O called ?
(ii) OR and OQ are perpendiculars drawn to AB and CA respectively. What is the relation between OR and OQ ?
(iii) What is relation between angle ACO and angle BCO ?
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
(i) What do you call the point O ?
(ii) What is the relation between the distances OA, OB and OC ?
(iii) Does the perpendicular bisector of BC pass through O ?
Using ruler and compasses only,
(i) Construct triangle ABC, having given BC = 7 cm, AB - AC = 1 cm and ∠ABC = 45°.
(ii) Inscribe a circle in the △ABC constructed in (i) above.
Using ruler and compasses only,
(i) Construct a triangle ABC with the following data :
Base AB = 6 cm, BC = 7.5 cm and angle CAB = 60°.
(ii) In same diagram, draw a circle which passes through the points A, B and C and mark its center O.
(iii) Draw a perpendicular from O to AB which meets AB in D.
(iv) Prove that : AD = BD.