Mathematics
Use a graph for this question. Draw an ogive for the given distribution. From the graph determine :
(i) the median
| Marks | No. of students |
|---|---|
| 0-10 | 5 |
| 10-20 | 10 |
| 20-30 | 14 |
| 30-40 | 21 |
| 40-50 | 25 |
| 50-60 | 34 |
| 60-70 | 36 |
| 70-80 | 27 |
| 80-90 | 16 |
| 90-100 | 12 |
(ii) the number of students scoring above 65 marks.
(iii) if 10 students qualify for merit scholarship, find the minimum marks required to qualify.
(iv) the number of students who did not pass, if the pass percentage was 35.
Statistics
6 Likes
Answer
Cumulative frequency table is shown below:
| Marks | No. of students | Cumulative frequency |
|---|---|---|
| 0-10 | 5 | 5 |
| 10-20 | 10 | 15 |
| 20-30 | 14 | 29 |
| 30-40 | 21 | 50 |
| 40-50 | 25 | 75 |
| 50-60 | 34 | 109 |
| 60-70 | 36 | 145 |
| 70-80 | 27 | 172 |
| 80-90 | 16 | 188 |
| 90-100 | 12 | 200 |
Steps of construction :
Take 1 cm along x-axis = 10 (marks)
Take 1 cm along y-axis = 20 (students)
Plot the points (10, 5), (20, 15), (30, 29), (40, 50), (50, 75), (60, 109), (70, 145), (80, 172), (90, 188) and (100, 200) representing upper class limits and the respective cumulative frequencies. Also plot the point representing lower limit of the first class i.e., 0 - 10.
Join these points by a freehand drawing.
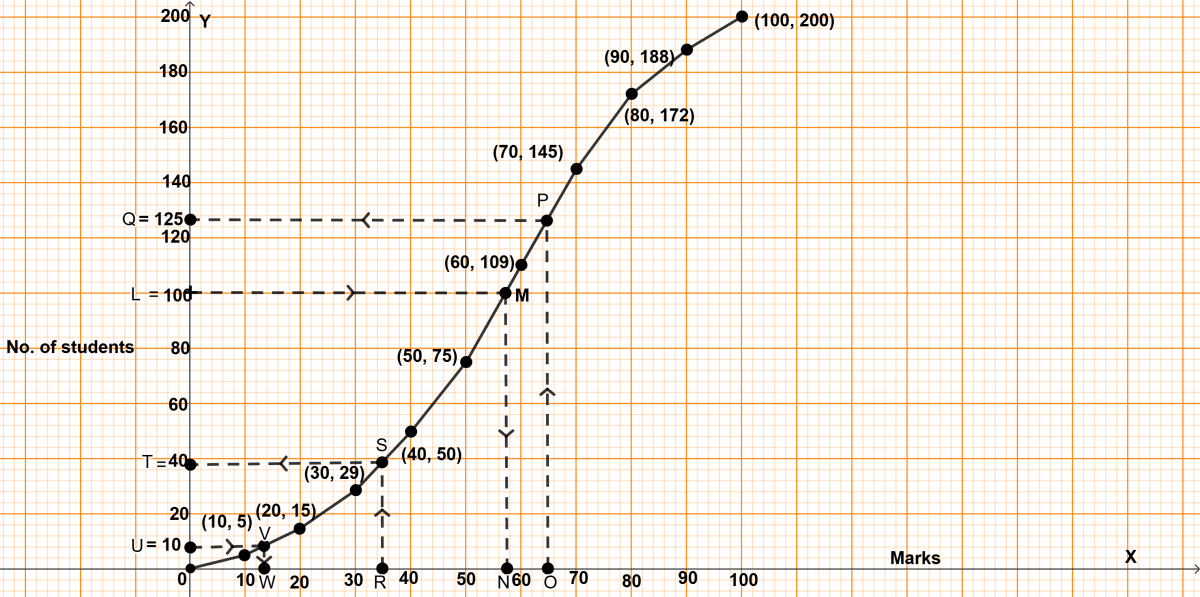
(i) Total no. of students = 200, which is even.
Median = = 100th term.
Through L = 100, draw a horizontal line to meet the ogive at M. Through M, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 57.
Hence, the median marks = 57.
(ii) Let O be the point on x-axis representing marks = 65.
Through O draw a vertical line to meet the ogive at P. Through P, draw a horizontal line to meet the y-axis at Q. The ordinate of the point Q represents 125.
Hence, 125 students score less than 65 so students scoring more than 65 = 200 - 125 = 75.
Hence, 75 students score more than 65 marks in the test.
(iii) Through U = 10, draw a horizontal line to meet the ogive at V. Through V, draw a vertical line to meet the x-axis at W. The abscissa of the point W represents 12.
Hence, minimum marks required to qualify = 12.
(iv) Total marks = 100
35% of 100 = 35.
Let R be the point on x-axis representing marks = 35.
Through R, draw a vertical line to meet the ogive at S. Through S, draw a horizontal line to meet the y-axis at T. The ordinate of the point T represents 38.
No. of students who scored less than 35 marks = 38.
Hence, 38 students failed in the examination.
Answered By
3 Likes
Related Questions
If a, b and c are in continued proportion, prove that :
abc(a + b + c)3 = (ab + bc + ca)3.
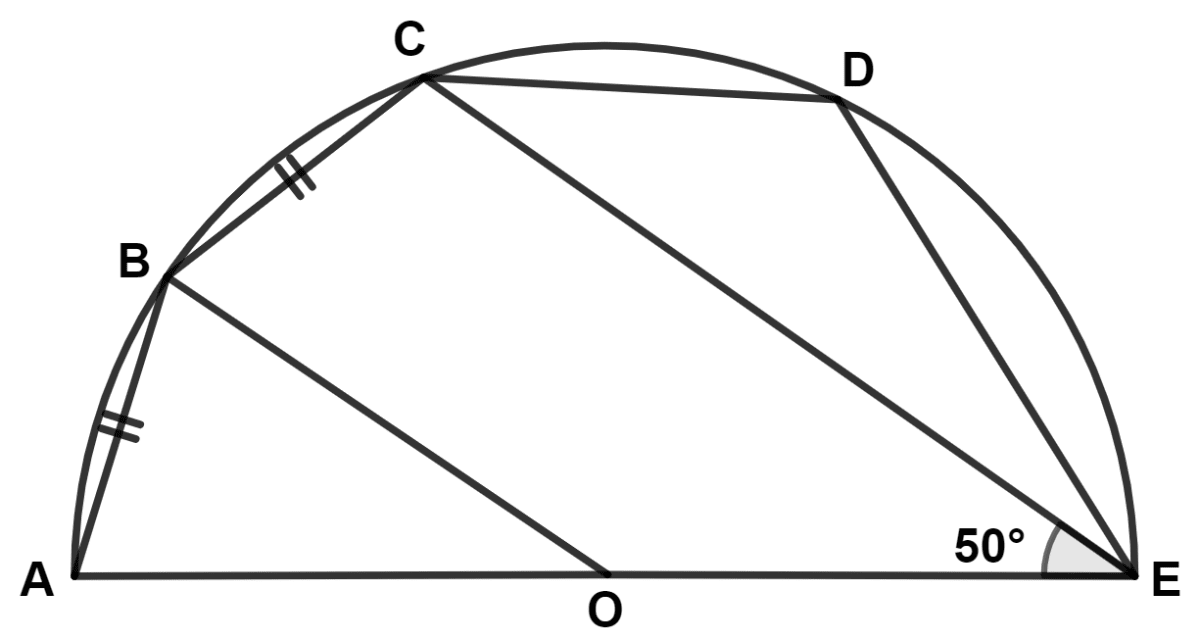
The given figure shows a semicircle with center at point O and AE as diameter. Chord AB = chord BC and angle CEO = 50°.
(i) Find angle AOB.
(ii) Show that OB is parallel to EC.
If matrix A = }[r] 1 & 2 \ 2 & 1 \end{bmatrix} and I is a unit matrix of order 2; find the value of m so that :
A2 - 2A - mI = 0
The quadratic equation x2 + x + p = 0 has real and distinct roots, find the value of p.