Mathematics
Two trains leave a railway station at same time. The first train travels due west and the second train due north. The first train travels 5 km/hr faster than the second train. If after 2 hours, they are 50 km apart, find the speed of each train.
Quadratic Equations
15 Likes
Answer
Let speed of second train be x km/hr and first be (x + 5) km/hr.
According to figure,
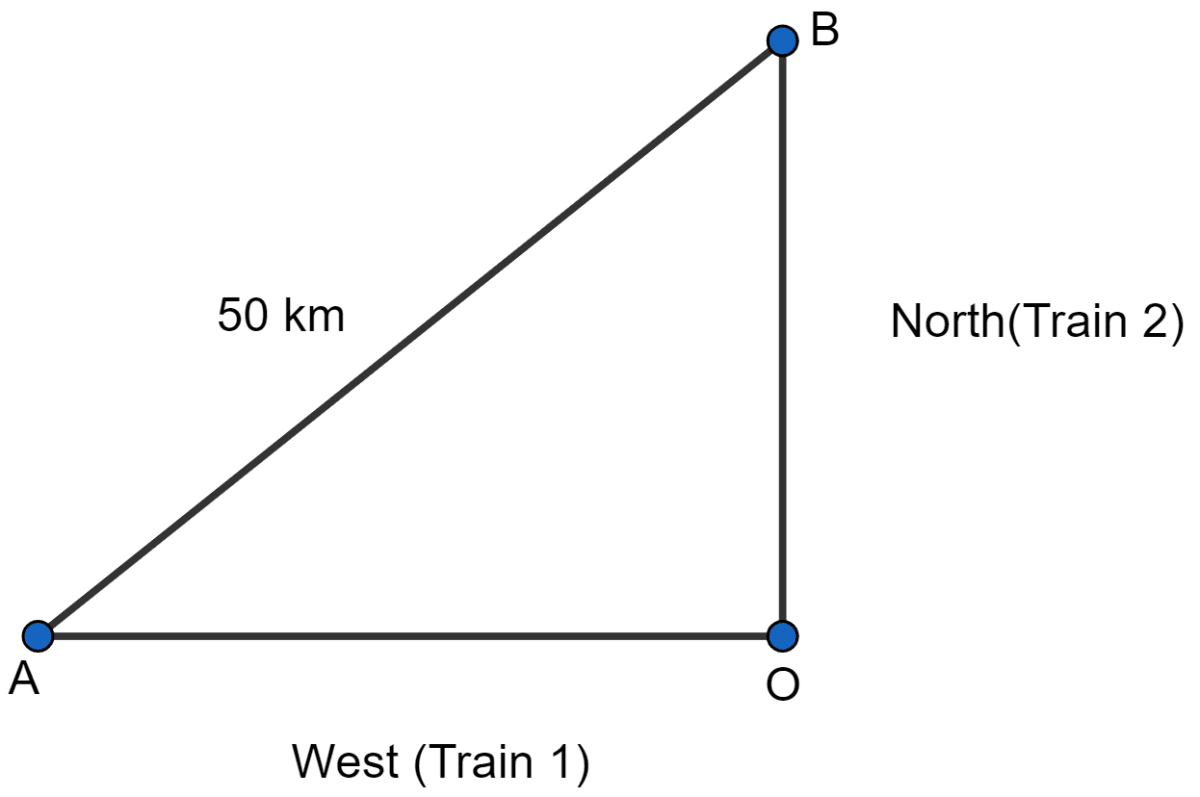
Let O be the position where trains leave
Distance travelled by first train OA = 2(x + 5) km
Distance travelled by second train OB = 2x km
By pythagoras theorem we get,
⇒ AB2 = OA2 + OB2
⇒ 502 = [2(x + 5)]2 + (2x)2
⇒ 502 = 4(x + 5)2 + 4x2
⇒ 2500 = 4(x2 + 25 + 10x) + 4x2
⇒ 2500 = 4x2 + 100 + 40x + 4x2
⇒ 8x2 + 40x - 2400 = 0
⇒ 8(x2 + 5x - 300) = 0
⇒ x2 + 5x - 300 = 0
⇒ x2 + 20x - 15x - 300 = 0
⇒ x(x + 20) - 15(x + 20) = 0
⇒ (x - 15)(x + 20) = 0
⇒ x - 15 = 0 or x + 20 = 0
⇒ x = 15 or x = -20.
Since, speed cannot be negative,
∴ x ≠ -20.
∴ x = 15 and x + 5 = 20
Hence, speed of first train = 20 km/hr and second train = 15 km/hr.
Answered By
10 Likes
Related Questions
An aeroplane covered a distance of 400 km at an average speed of x km/h. On the return journey, the speed was increased by 40 km/h . Write down an expression for the time taken for :
(i) the onward journey
(ii) the return journey
If the return journey took 30 minutes less than the onward journey , write down an equation in x and find its value.
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away in time, it has to increase its speed by 250 km/hr from its usual speed. Find its usual speed.
The sum of the ages of a father and his son is 45 years. Five years ago, the product of their ages (in years) was 124. Determine their present ages.
In an auditorium, seats were arranged in rows and columns. The number of rows was equal to number of seats in each row. When the number of rows was doubled and the number of seats in each row was reduced by 10, the total number of seats increased by 300. Find :
(i) the number of rows in the original arrangement.
(ii) the number of seats in the auditorium after re-arrangement.