Mathematics
Two chords AB, CD of a circle intersect internally at a point P. If
(i) AP = 6 cm, PB = 4 cm and PD = 3 cm, find PC.
(ii) AB = 12 cm, AP = 2 cm, PC = 5 cm, find PD.
(iii) AP = 5 cm, PB = 6 cm and CD = 13 cm, find CP.
Circles
28 Likes
Answer
We know that when two chords of a circle intersect internally or externally, then the products of the lengths of segments are equal.
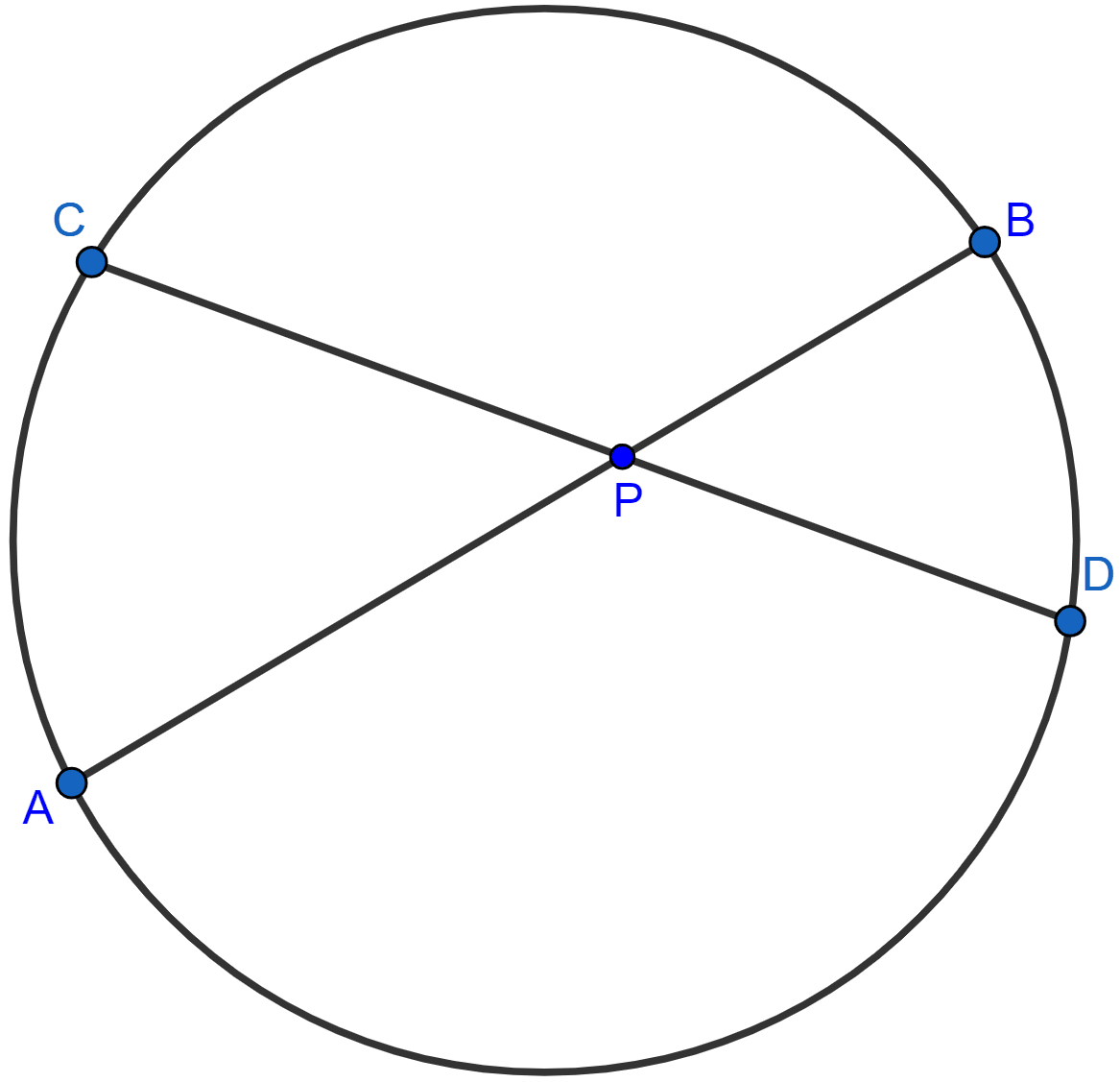
Given, chords AB and CD of a circle intersect internally at a point P. So,
PA.PB = PC.PD
(i) Given, AP = 6 cm, PB = 4 cm and PD = 3 cm.
We know that,
PA.PB = PC.PD
⇒ 6 × 4 = PC × 3
⇒ 24 = 3PC
⇒ PC = = 8 cm.
Hence, the length of PC = 8 cm.
(ii) Given, AB = 12 cm, AP = 2 cm, PC = 5 cm
PB = AB - AP = 12 - 2 = 10 cm.
We know that,
PA.PB = PC.PD
⇒ 2 × 10 = 5 × PD
⇒ 20 = 5PD
⇒ PD = = 4 cm.
Hence, the length of PD = 4 cm.
(iii) Given, AP = 5 cm, PB = 6 cm and CD = 13 cm
Let PC = x, so PD = 13 - x
We know that,
PA.PB = PC.PD
⇒ 5 × 6 = x(13 - x)
⇒ 30 = 13x - x2
⇒ x2 - 13x + 30 = 0
⇒ x2 - 10x - 3x + 30 = 0
⇒ x(x - 10) - 3(x - 10) = 0
⇒ (x - 3)(x - 10) = 0
⇒ x - 3 = 0 or x - 10 = 0
⇒ x = 3 or x = 10.
Hence, PC = 3 cm or 10 cm.
Answered By
15 Likes
Related Questions
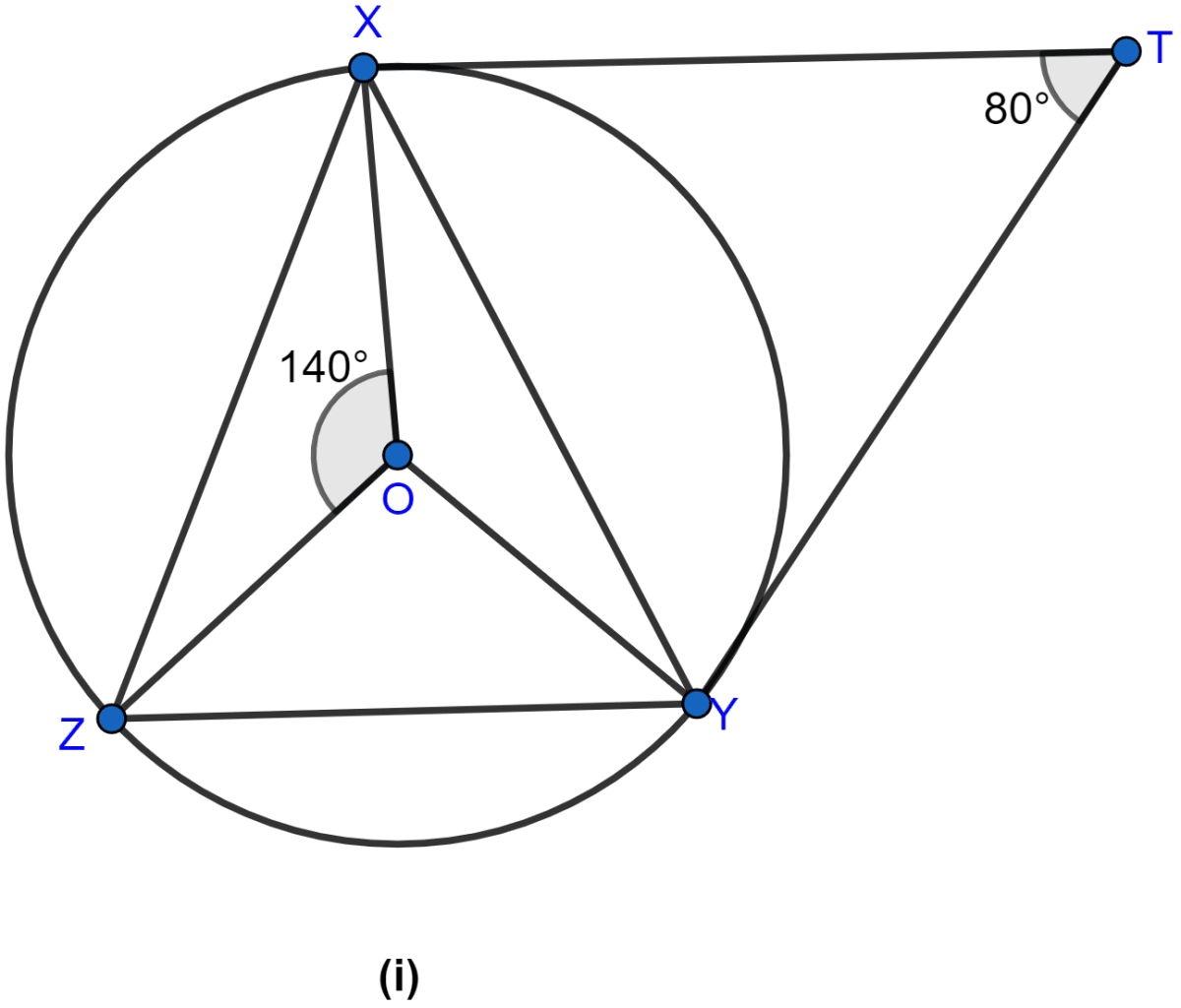
In the figure (i) given below, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
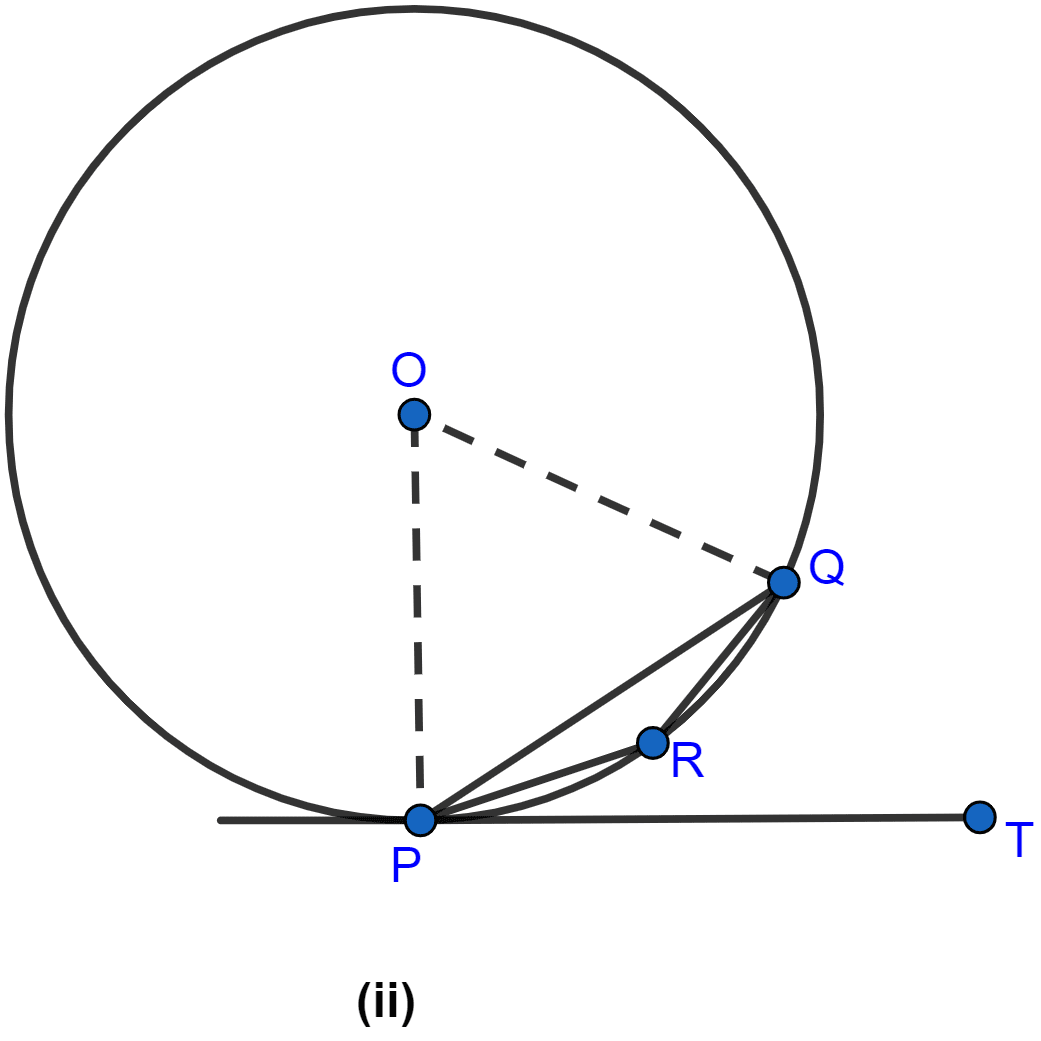
In the figure (ii) given below, O is the center of the circle and PT is the tangent to the circle at P. Given ∠QPT = 30°, calculate
(i) ∠PRQ
(ii) ∠POQ.
In the figure (i) given below, PT is a tangent to the circle. Find TP if AT = 16 cm and AB = 12 cm.

In the figure (ii) given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find :
(i) AB
(ii) the length of tangent PT.
