Triangle OA₁B₁ is the reflection of triangle OAB in origin, where A₁ (4, -5) is the image of A and B₁ (-7, 0) is the image of B.

``` kboatpngend

(i) Write down the co-ordinates of A and B and draw a diagram to represent this information.

(ii) Give a special name to the quadrilateral ABA<sub>1</sub>B<sub>1</sub>. Give reason.

(iii) Find the co-ordinates of A<sub>2</sub>, the image of A under reflection in x-axis followed by reflection in y-axis.

(iv) Find the co-ordinates of B<sub>2</sub>, the image of B under reflection in y-axis followed by reflection in origin.

(i) From graph,

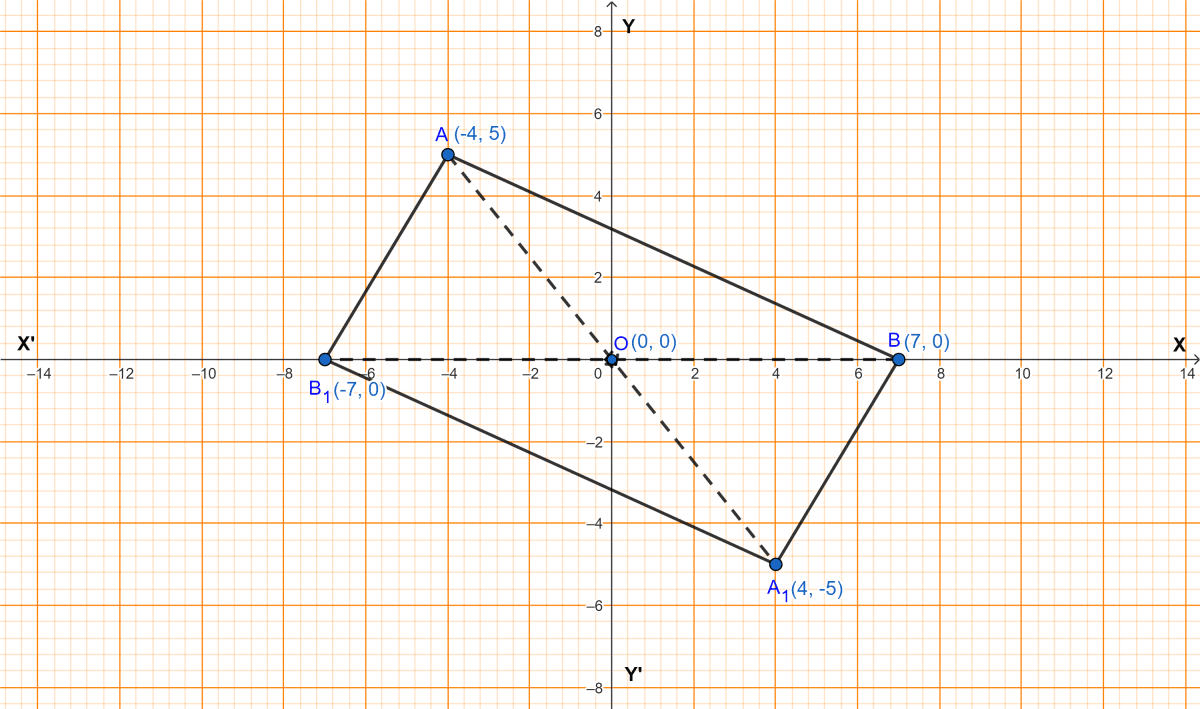
Coordinates of A = (-4, 5) and B = (7, 0).

(ii) By distance formula,

OA = $\sqrt{(-4 - 0)^2 + (5 - 0)^2} = \sqrt{(-4)^2 + 5^2} = \sqrt{16 + 25} = \sqrt{41}$ units.

OA<sub>1</sub> = $\sqrt{(4 - 0)^2 + (-5 - 0)^2} = \sqrt{16 + 25} = \sqrt{41}$ units.

OB = OB<sub>1</sub> = 7 units.

Since, diagonals bisect each other.

Hence, ABA<sub>1</sub>B<sub>1</sub> is a parallelogram.

(iii) We know that,

On reflection in x-axis, the sign of y-coordinate changes.

∴ (-4, 5) on reflection in x-axis gives (-4, -5).

We know that,

On reflection in y-axis, the sign of x-coordinate changes.

∴ (-4, -5) on reflection in y-axis gives (4, -5).

∴ A<sub>2</sub> = (4, -5).

Hence, coordinates of A<sub>2</sub> = (4, -5).

(iv) We know that,

On reflection in y-axis, the sign of x-coordinate changes.

∴ (7, 0) on reflection in y-axis gives (-7, 0).

We know that,

On reflection in x-axis, the sign of y-coordinate changes.

∴ (-7, 0) on reflection in x-axis gives (-7, 0).

∴ B<sub>2</sub> = (-7, 0).

Hence, coordinates of B<sub>2</sub> = (-7, 0).