Mathematics
From the top of a 80 m high tower, the angles of depression of two men, on either sides of the tower, are found to be 32° and 58°. Find the distance between the two men correct to the nearest whole numbers.
Heights & Distances
9 Likes
Answer
Let AB be the tower and C and D be the position of two different men.
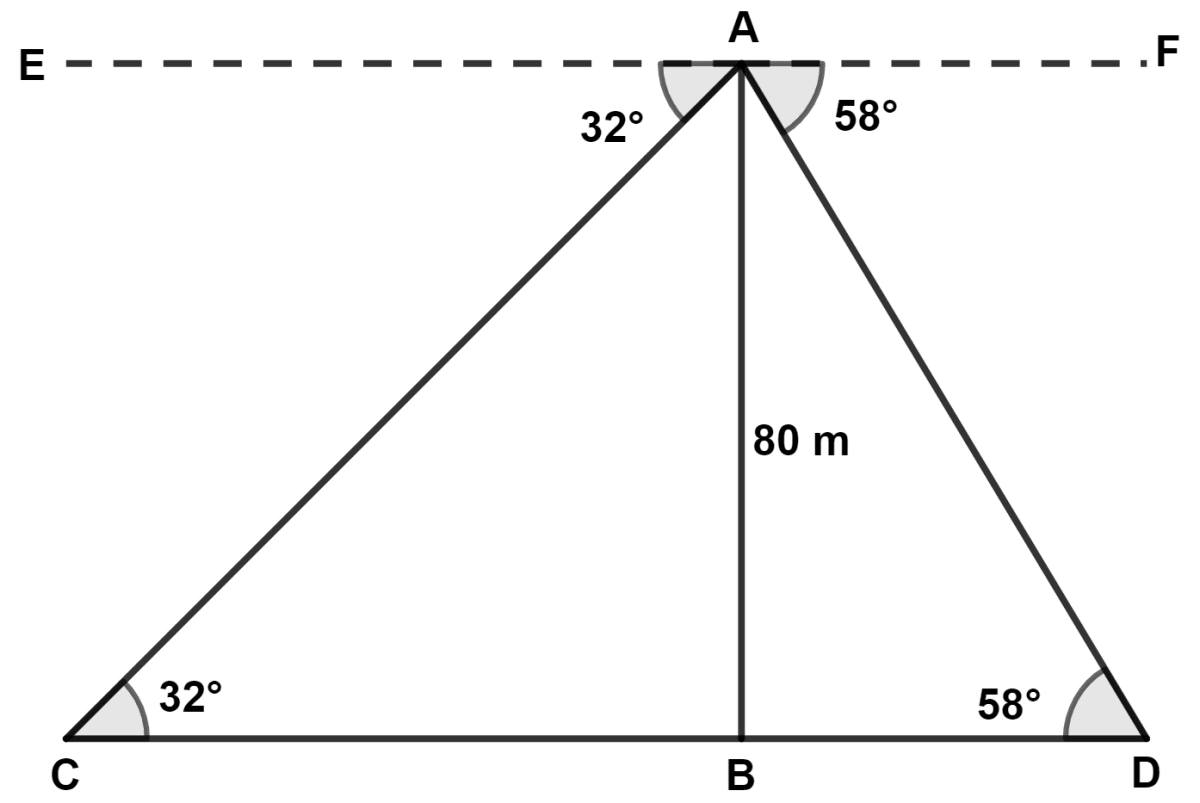
From figure,
⇒ ∠ACB = ∠EAC = 32° (Alternate angles are equal)
⇒ ∠ADB = ∠FAD = 58° (Alternate angles are equal)
In △ ABD,
⇒ tan 58° =
⇒ 1.6003 =
⇒ BD = = 49.99 ≈ 50 m.
In △ ABC,
⇒ tan 32° =
⇒ 0.6249 =
⇒ BC = = 128.06 ≈ 128 m.
From figure,
CD = BC + BD = 128 + 50 = 178 m.
Hence, distance between two men = 178 m.
Answered By
6 Likes
Related Questions
A cylindrical ice-cream container, completely filled with ice-cream has 22 cm radius and 24 cm height. If this ice-cream is to be distributed among some children by filling it in the cone of radius 2 cm, height 7 cm and upper part of the cone which is hemisphere, then how many children will get the ice-cream cones?
The equation of a line is 7 - 3x - 4y = 0. Find :
(i) the slope of the line
(ii) the equation of the line perpendicular to the given line and passing through the intersection of the lines x - y + 2 and 3x + y - 10 = 0.
Find the smallest value of x for the inequation x - 3(2 + x) < 2(3x - 1) when :
(i) x ∈ W (whole numbers)
(ii) x ∈ N (natural numbers)
(iii) x ∈ I (integers)
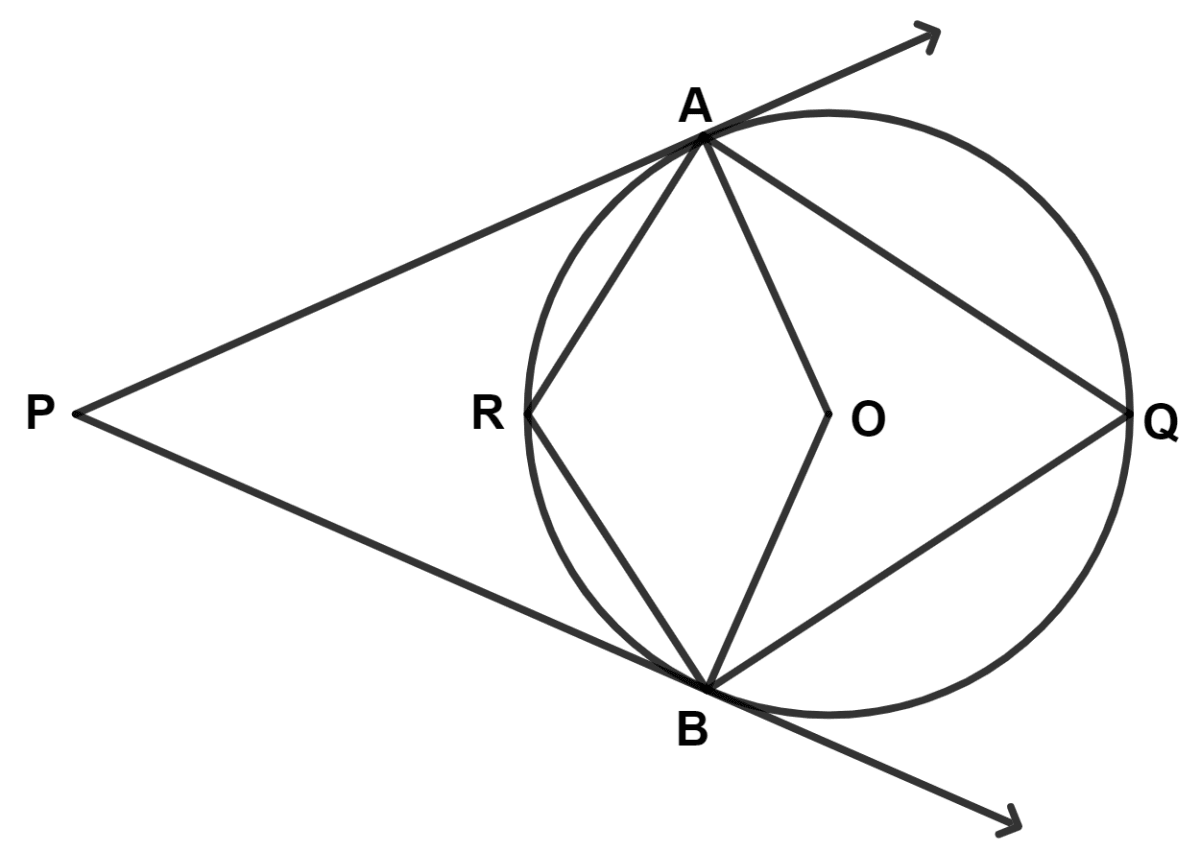
In the given figure, PA and PB are tangents at the points A and B respectively of a circle with center O. Q and R are points on the circle, if ∠APB = 70°, find :
(i) reflex angle AOB
(ii) ∠AQB
(iii) ∠ARB