Mathematics
The shaded region of the given diagram represents the lawn in front of a house. On three sides of the lawn there are flower beds of width 2 m.
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower–beds.

Answer
(i) Let PQRS be the lawn.
From figure,
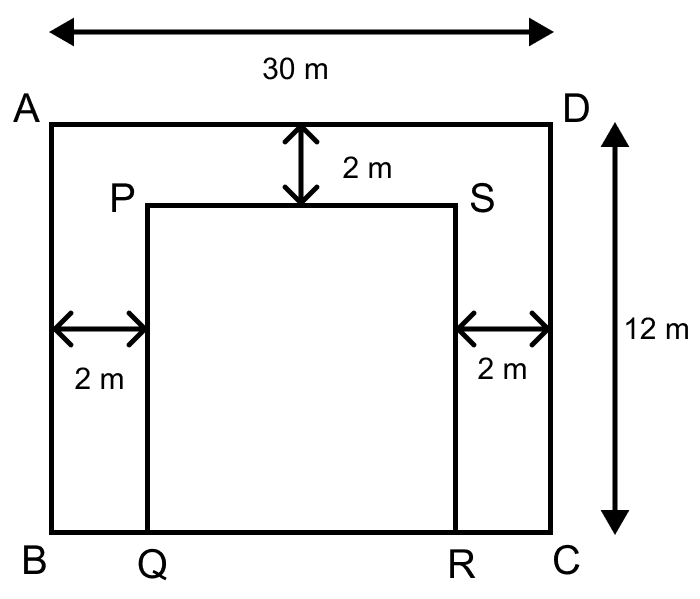
QR = BC - BQ - RC = 30 - 2 - 2 = 26 m.
SR = CD - DS = 12 - 2 = 10 m.
Length of PQRS = QR = 26 m and,
Breadth of PQRS = SR = 10 m.
Hence, length and breadth of lawn are 26 m and 10 m respectively.
(ii) From figure,
Area of flower beds = Area of rectangle ABCD - Area of rectangle PQRS
= (AD × DC) - (QR × SR)
= (30 × 12) - (26 × 10)
= 360 - 260
= 100 m2.
Hence, area of flower-beds = 100 m2.
Related Questions
In the diagram (ii) given below, calculate the area of the shaded portion. All measurements are in centimetres.

A rectangular plot 20 m long and 14 m wide is to be covered with grass leaving 2 m all around. Find the area to be laid with grass.
A foot path of uniform width runs all around the inside of a rectangular field 50 m long and 38 m wide. If the area of the path is 492 m2, find its width.
The cost of enclosing a rectangular garden with a fence all around at the rate of ₹15 per metre is ₹5400. If the length of the garden is 100 m, find the area of the garden.