Mathematics
The shaded region of the given diagram represents the lawn in front of a house. On three sides of the lawn there are flower beds of width 2 m.
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower–beds.

Answer
(i) Let PQRS be the lawn.
From figure,
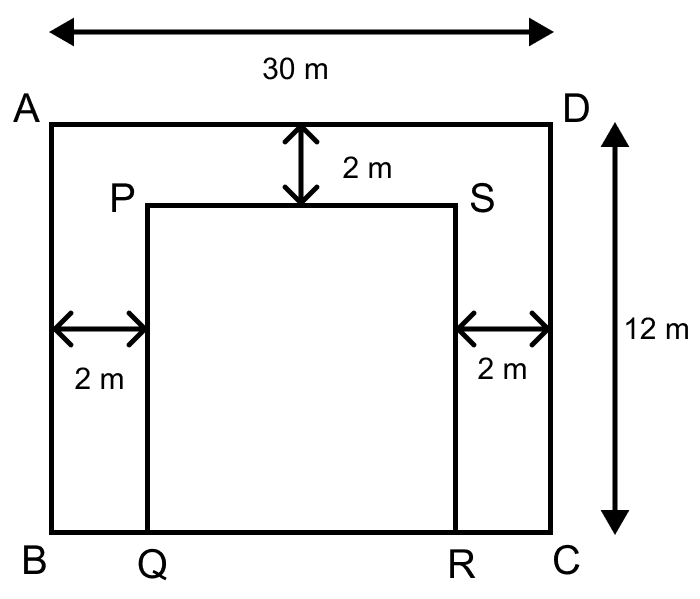
QR = BC - BQ - RC = 30 - 2 - 2 = 26 m.
SR = CD - DS = 12 - 2 = 10 m.
Length of PQRS = QR = 26 m and,
Breadth of PQRS = SR = 10 m.
Hence, length and breadth of lawn are 26 m and 10 m respectively.
(ii) From figure,
Area of flower beds = Area of rectangle ABCD - Area of rectangle PQRS
= (AD × DC) - (QR × SR)
= (30 × 12) - (26 × 10)
= 360 - 260
= 100 m2.
Hence, area of flower-beds = 100 m2.
Related Questions
The cost of enclosing a rectangular garden with a fence all around at the rate of ₹15 per metre is ₹5400. If the length of the garden is 100 m, find the area of the garden.
In the diagram (ii) given below, calculate the area of the shaded portion. All measurements are in centimetres.

A rectangular plot 20 m long and 14 m wide is to be covered with grass leaving 2 m all around. Find the area to be laid with grass.
A foot path of uniform width runs all around the inside of a rectangular field 50 m long and 38 m wide. If the area of the path is 492 m2, find its width.