Mathematics
The sequence 2, 9, 16, ….. is given.
(a) Identify if the given sequence is an AP or a GP. Give reasons to support your answer.
(b) Find the 20th term of the sequence.
(c) Find the difference between the sum of its first 22 and 25 terms.
(d) Is the term 102 belong to this sequence?
(e) If ‘k’ is added to each of the above terms, will the new sequence be in A.P. or G.P.?
AP GP
25 Likes
Answer
(a) Difference between common terms : 16 - 9 = 9 - 2 = 7.
Since, difference between common terms are equal.
Hence, the given sequence is an A.P.
(b) By formula,
an = a + (n - 1)d
a20 = 2 + (20 - 1) × 7
= 2 + 19 × 7
= 2 + 133
= 135.
Hence, 20th term of the sequence = 135.
(c) By formula,
Sn =
Substituting values we get :
Sum upto 22 terms :
Sum upto 25 terms :
S25 - S22 = 2150 - 1661 = 489.
Hence, difference between the sum of its first 22 and 25 terms = 489.
(d) Let nth term be 102.
⇒ an = a + (n - 1)d
⇒ 102 = 2 + 7(n - 1)
⇒ 102 = 2 + 7n - 7
⇒ 102 = 7n - 5
⇒ 102 + 5 = 7n
⇒ 7n = 107
⇒ n = .
Since, n cannot be in fraction.
Hence, 102 is not the term of the sequence.
(e) If k is added to each term.
Sequence : 2 + k, 9 + k, 16 + k,………….
The common difference between terms is still equal to 7.
Hence, sequence is in A.P.
Answered By
14 Likes
Related Questions
On seeing the below display board outside Pearl Stationary Shop, Chetan enters the shop to buy the following items:

Pen Pencil Rainbow cover notebook Price ₹5 each ₹7 each ₹ 200 each Discount 5% on a dozen pens 10% on 20 pencils ------ Premium - - ₹50 on each notebook Items purchased 1 dozen 20 pencils 5 GST 18% 12% 12% The shopkeeper handed over the bill to Chetan saying that he has given further discount of 2% on total bill. Chetan became so happy hearing about the discount that he did not check the bill until he reached home. He later found out that though shopkeeper has given 2% discount as promised, he had also mischarged uniform 18% GST on all the items.
(a) Calculate :
(i) total selling price of all the items as per the offers displayed on the board.
(ii) total amount to be paid by Chetan including GST with correct rates.
(iii) actual amount charged by the shopkeeper.
(b) Did the shopkeeper overcharge Chetan? Justify your answer
Using remainder and factor theorem, show that (2x + 3) is a factor of the polynomial 2x2 + 11x + 12. Hence, factorise it completely. What must be multiplied to the given polynomial so that x2 + 3x - 4 is a factor of the resulting polynomial? Also, write the resulting polynomial.
Given the equations of two straight lines, L1 and L2 are x - y = 1 and x + y = 5 respectively. If L1 and L2 intersects at point Q (3, 2). Find :
(a) the equation of line L3 which is parallel to L1 and has y-intercept 3.
(b) the value of k, if the line L3 meets the line L2 at a point P (k, 4).
(c) the coordinate of R and the ratio PQ : QR, if line L2 meets x-axis at point R.
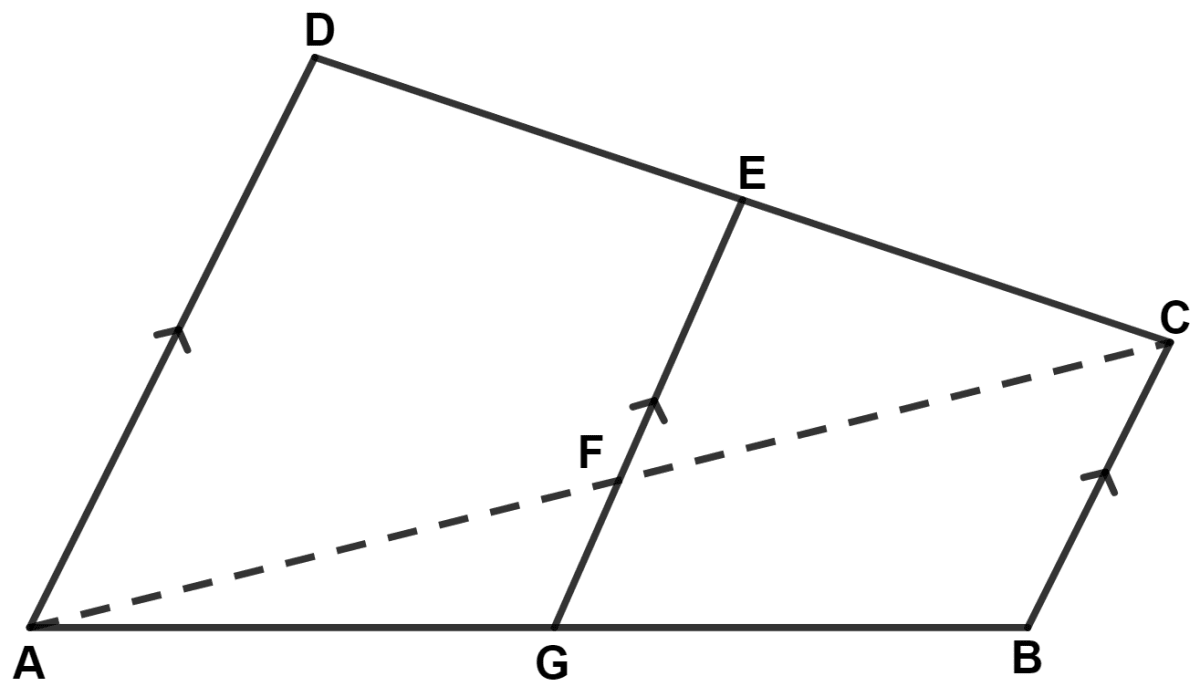
In the figure given below (not drawn to scale), AD ∥ GE ∥ BC, DE = 18 cm, EC = 3 cm, AD = 35 cm. Find :
(a) AF : FC
(b) length of EF
(c) area(trapezium ADEF) : area(Δ EFC)
(d) BC ∶ GF