Mathematics
The points (6, 2), (3, -1) and (-2, 4) are the vertices of a right angled triangle. Check whether it remains a right angled triangle after reflection in the y-axis.
Reflection
11 Likes
Answer
The right angled triangle with points (6, 2), (3, -1) and (-2, 4) as vertices is plotted below:
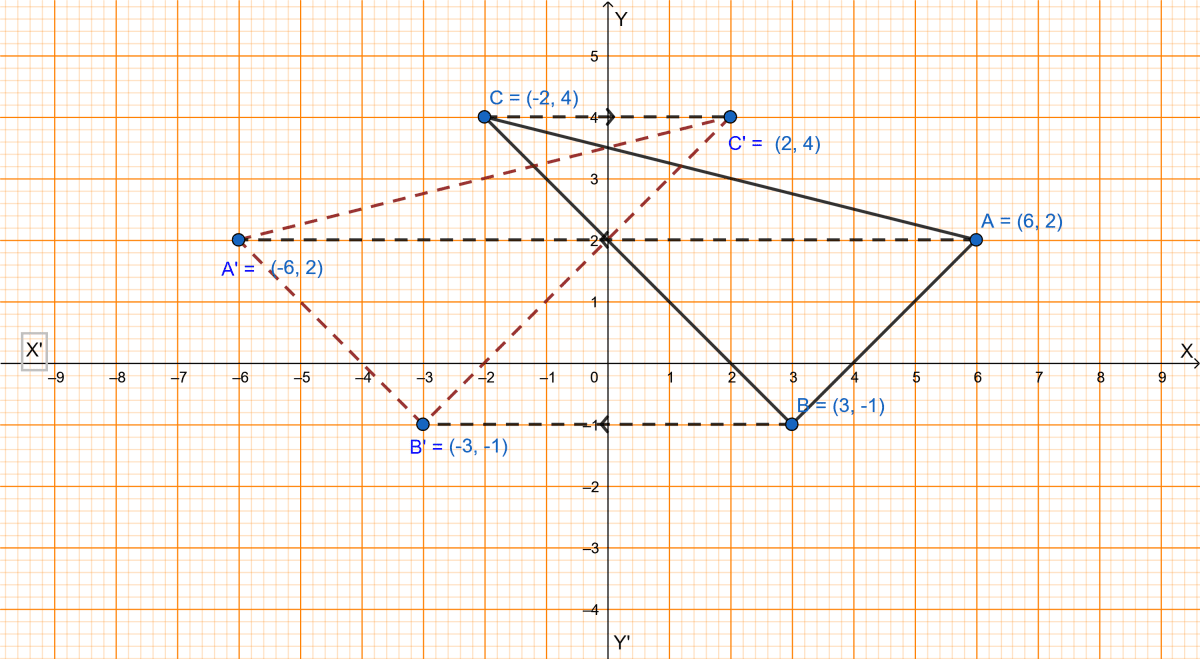
From graph we get,
AB = A'B'
AC = A'C'
BC = B'C'
∴ △ABC and △A'B'C' are congruent.
Since, △ABC is a right angled triangle hence, △A'B'C' is also a right angled triangle.
Answered By
8 Likes
Related Questions
The image of a point P on reflection in a line l is a point P'. Describe the location of the line l.
Plot the points A(2, -3), B(-1, 2) and C(0, -2) on the graph paper. Draw the triangle formed by reflecting these points in the x-axis. Are the two triangles congruent ?
Points A and B have coordinates (2, 5) and (0, 3). Find :
(i) the image A' of A under reflection in the x-axis.
(ii) the image B' of B under reflection in the line AA'.
The triangle ABC where A(1, 2), B(4, 8), C(6, 8) is reflected in the x-axis to triangle A'B'C'. The triangle A'B'C' is then reflected in the origin to the triangle A''B''C''. Write down the coordinates of A'', B'', C''. Write down a single transformation that maps ABC onto A''B''C''.