Mathematics
The point P(3, 4) is reflected to P' in the x-axis and O' is the image of O(origin) in the line PP'. Find :
(i) the coordinates of P' and O'.
(ii) the length of segments PP' and OO'.
(iii) the perimeter of the quadrilateral POP'O'.
(iv) the geometrical name of the figure POP'O'.
Reflection
22 Likes
Answer
The graph is shown below:
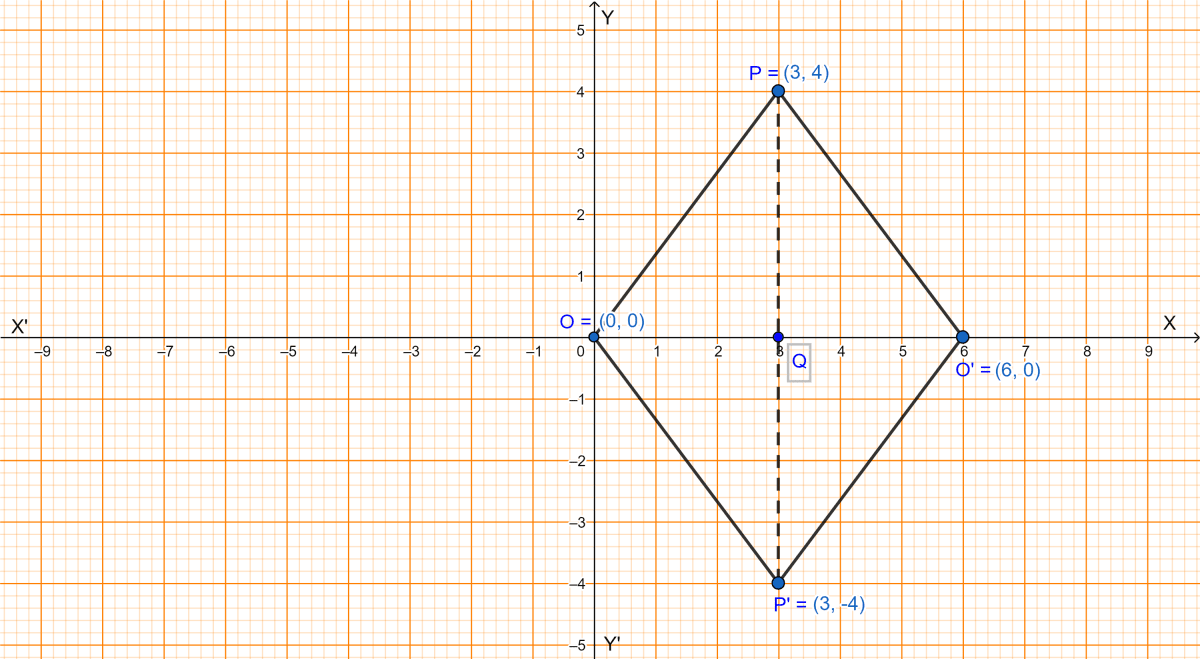
(i) From graph we get,
The coordinates of P' and O' are (3, -4) and (6, 0) respectively.
(ii) From graph we get,
Length of PP' = 8 units and OO' = 6 units.
(iii) OP = PO' = O'P' = P'O, as all are hypotenuse for same base and perpendicular.
∴ Perimeter of POP'O' is = 4 × OP
The perimeter of the quadrilateral POP'O' is 20 units.
(iv) POP'O' is a rhombus.
Answered By
8 Likes
Related Questions
Use graph paper to solve this question.
(i) Plot the points A(4, 6) and B(1, 2).
(ii) If A' is the image of A when reflected in the x-axis, write the coordinates of A'.
(iii) If B' is the image of B when reflected in the line AA', write the coordinates of B'.
(iv) Give the geometrical name for the figure ABA'B'.
The points A(2, 3), B(4, 5) and C(7, 2) are the vertices of △ABC.
(i) Write down the coordinates of A1, B1, C1 if △A1B1C1 is the image of △ABC when reflected in the origin.
(ii) Write down the coordinates of A2, B2, C2 if △A2B2C2 is the image of △ABC when reflected in the x-axis.
(iii) Assign the special name to quadrilateral BCC2B2 and find its area.
Using a graph paper, plot the points A(6, 4) and B(0, 4).
(i) Reflect A and B in the origin to get images A' and B'.
(ii) Write the coordinates of A' and B'.
(iii) State the geometrical name for the figure ABA'B'.
(iv) Find its perimeter.
Use a graph paper for this question. (Take 10 small divisions = 1 unit on both axes). P and Q have coordinates (0, 5) and (-2, 4).
(i) P is invariant when reflected in an axis. Name the axis.
(ii) Find the image of Q on reflection in the axis found in (i).
(iii) (0, k) on reflection in the origin is invariant. Write the value of k.
(iv) Write the coordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis.