The line 4x + 5y + 20 = 0 meets x-axis at point A and y-axis at point B. Find :

(i) the coordinates of points A and B.

(ii) the co-ordinates of point P in AB such that AB : BP = 5 : 3.

(iii) the equation of the line through P and perpendicular to AB.

(i) We know that,

y-coordinate at x-axis = 0.

Substituting y = 0 in 4x + 5y + 20 = 0, we get :

⇒ 4x + 5(0) + 20 = 0

⇒ 4x = -20

⇒ x = -5.

A = (-5, 0).

x-coordinate at y-axis = 0.

Substituting x = 0 in 4x + 5y + 20 = 0, we get :

⇒ 4(0) + 5y + 20 = 0

⇒ 5y = -20

⇒ y = $\dfrac{-20}{5}$

⇒ y = -4.

B = (0, -4).

Hence, A = (-5, 0) and B = (0, -4).

(ii) Given,

AB : BP = 5 : 3

Let AB = 5a and BP = 3a.

From figure,

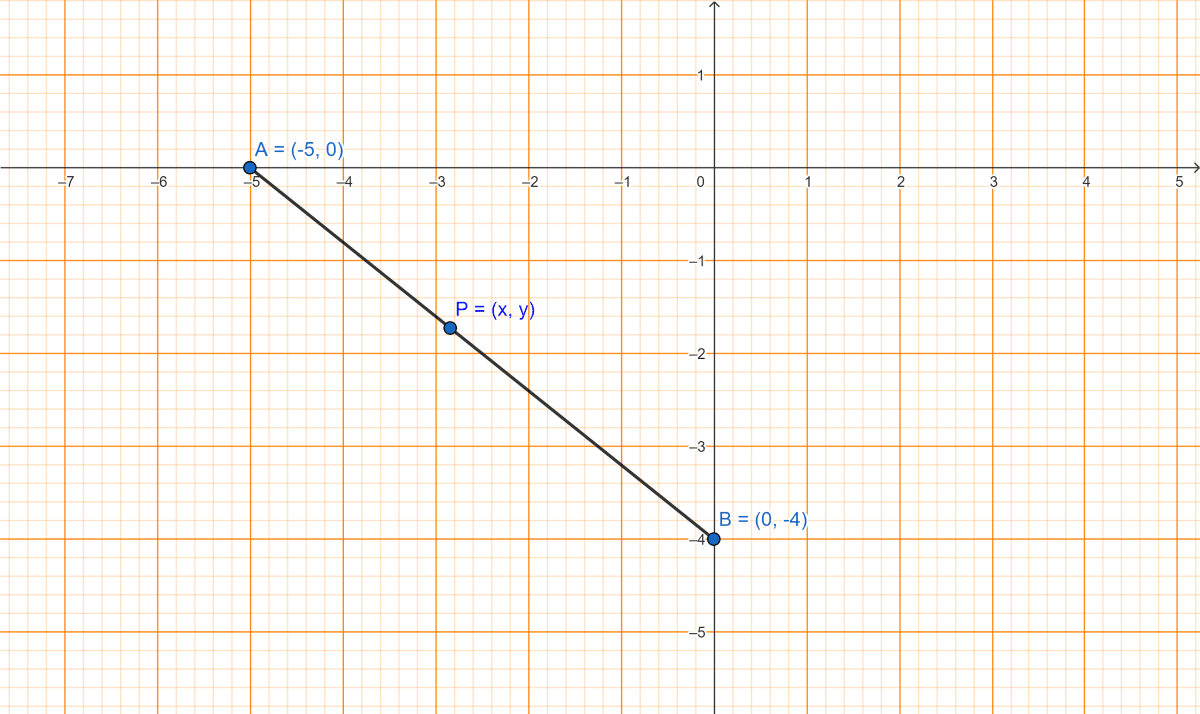
⇒ AB = AP + PB

⇒ 5a = AP + 3a

⇒ AP = 5a - 3a = 2a.

AP : BP = 2a : 3a = 2 : 3.

Let coordinates of P be (x, y).

By section-formula,

(x, y) = $\Big(\dfrac{m$1x2 + m2x1}{m1 + m2}, \dfrac{m1y2 + m2y1}{m1 + m2}\Big)

Substituting values for x-coordinate we get :

$\Rightarrow x = \dfrac{2 \times 0 + 3 \times -5}{2 + 3} \\[1em] \Rightarrow x = \dfrac{0 - 15}{5} \\[1em] \Rightarrow x = \dfrac{-15}{5} \\[1em] \Rightarrow x = -3.$

Substituting values for y-coordinate we get :

$\Rightarrow y = \dfrac{2 \times -4 + 3 \times 0}{2 + 3} \\[1em] \Rightarrow y = \dfrac{-8 + 0}{5} \\[1em] \Rightarrow y = \dfrac{-8}{5} = -1\dfrac{3}{5}.$

P = (x, y) = $\Big(-3, -1\dfrac{3}{5}\Big)$.

(iii) By formula,

Slope = $\dfrac{y$2 - y1}{x2 - x1}

Substituting values we get :

Slope of AB = $\dfrac{-4 - 0}{0 - (-5)} = -\dfrac{4}{5}$

Let slope of line perpendicular to AB be m.

We know that,

Product of slope of perpendicular lines = -1.

$\therefore -\dfrac{4}{5} \times m = -1 \\[1em] \Rightarrow m = \dfrac{5}{4}.$

By point-slope form,

Equation of line : y - y₁ = m(x - x₁)

Substituting values we get :

$\Rightarrow y - \Big(-1\dfrac{3}{5}\Big) = \dfrac{5}{4}[x - (-3)] \\[1em] \Rightarrow y + \Big(\dfrac{8}{5}\Big) = \dfrac{5}{4}[x + 3] \\[1em] \Rightarrow \dfrac{5y + 8}{5} = \dfrac{5x + 15}{4} \\[1em] \Rightarrow 4(5y + 8) = 5(5x + 15) \\[1em] \Rightarrow 20y + 32 = 25x + 75 \\[1em] \Rightarrow 25x - 20y + 75 - 32 = 0 \\[1em] \Rightarrow 25x - 20y + 43 = 0$

Hence, equation of line through P and perpendicular to AB is 25x - 20y + 43 = 0.