Mathematics
The lengths of the diagonals of a rhombus are 16 cm and 12 cm. The length of the side of rhombus is
9 cm
10 cm
8 cm
20 cm
Pythagoras Theorem
5 Likes
Answer
Let AC = 16 cm and BD = 12 cm.
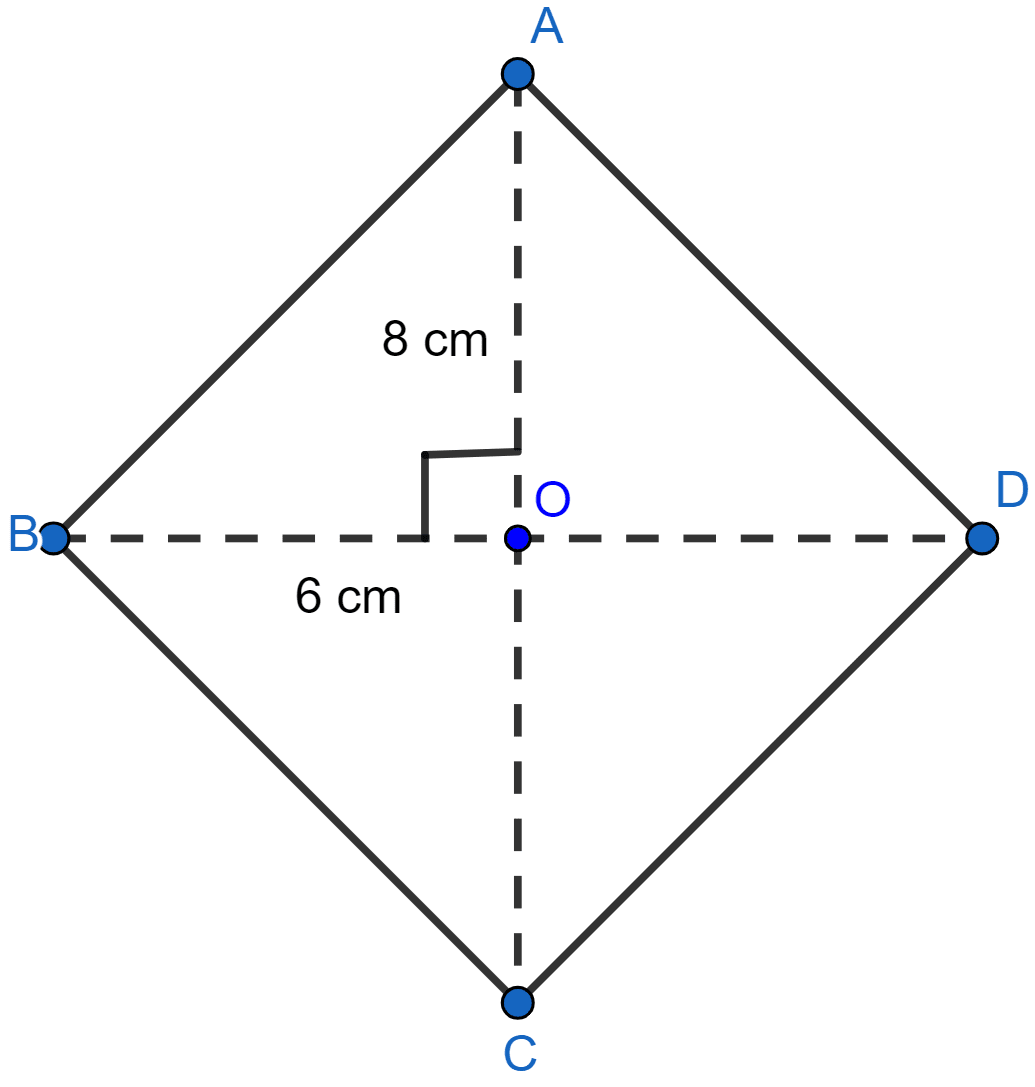
We know that,
Diagonals of rhombus are perpendicular and bisect each other,
OB = = 6 cm and AO = AC = 8 cm.
In right triangle AOB,
By pythagoras theorem we get,
⇒ AB2 = AO2 + OB2
⇒ AB2 = 82 + 62
⇒ AB2 = 64 + 36
⇒ AB2 = 100
⇒ AB = = 10 cm.
Hence, Option 2 is the correct option.
Answered By
2 Likes
Related Questions
In a △ABC, if AB = cm, BC = 6 cm and AC = 12 cm, then ∠B is
120°
90°
60°
45°
If the sides of a rectangular plot are 15 m and 8 m, then the length of its diagonal is
17 m
23 m
21 m
17 cm
If a side of a rhombus is 10 cm and one of the diagonals is 16 cm, then the length of the other diagonal is
6 cm
12 cm
20 cm
12 cm
If a ladder 10 m long reaches a window 8 m above the ground, then the distance of the foot of the ladder from the base of the wall is
18 m
8 m
6 m
4 m