Mathematics
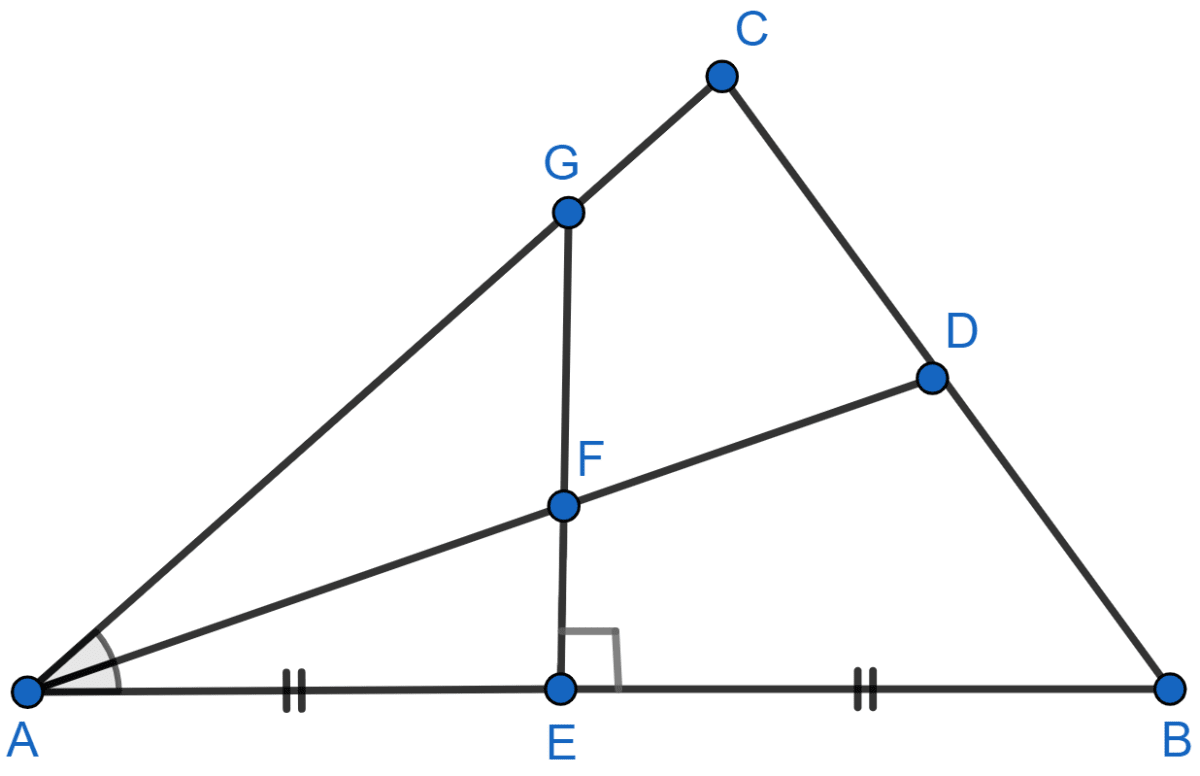
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F. Prove that :
(i) F is equidistant from A and B.
(ii) F is equidistant from AB and AC.
Locus
3 Likes
Answer
(i) Construct FB.
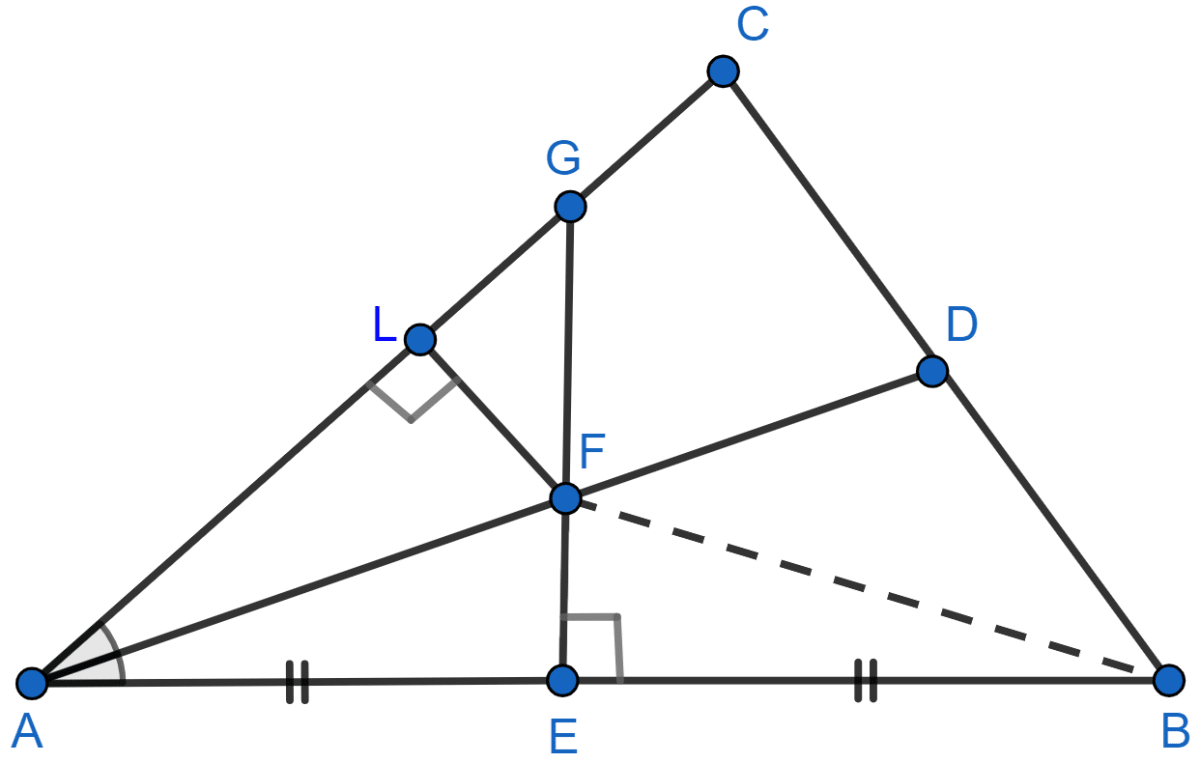
In △FAE and △FBE,
⇒ ∠FEA = ∠FEB [Both equal to 90°]
⇒ FE = FE [Common]
⇒ AE = EB [Given]
∴ △FAE ≅ △FBE by SAS axiom.
∴ FA = FB [By C.P.C.T.]
Hence, proved that F is equidistant from A and B.
(ii) Draw FL ⊥ AC.
In △FAL and △FAE,
⇒ ∠FLA = ∠FEA [Both equal to 90°]
⇒ FA = FA [Common]
⇒ ∠LAF = ∠FAE [Since, AD bisects ∠BAC]
∴ △FAL ≅ △FAE by AAS axiom.
∴ FL = FE [By C.P.C.T.]
Hence, proved that F is equidistant from AB and AC.
Answered By
3 Likes