Mathematics
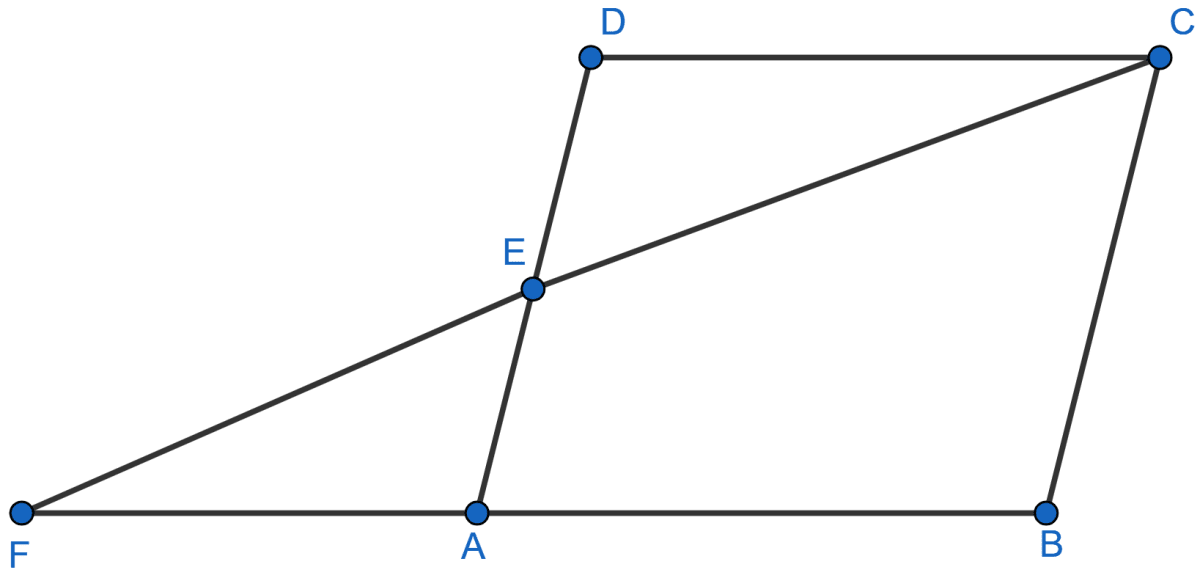
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
Similarity
11 Likes
Answer
From figure,
FB = AF + AB = 8 + 12 = 20 cm.
In △DEC and △EAF
⇒ ∠DEC = ∠FEA [Vertically opposite angles are equal]
⇒ ∠EDC = ∠EAF [Alternate angles are equal]
∴ △DEC ~ △EAF [By AA]
Since, corresponding sides of similar triangles are proportional we have :
Since, ABCD is a ||gm.
AB = CD and BC = AD.
From figure,
AD = AE + ED = 4 + 6 = 10 cm.
Perimeter of ||gm ABCD = AB + BC + CD + AD
= 12 + 10 + 12 + 10
= 44 cm.
Hence, perimeter of ||gm ABCD = 44 cm.
Answered By
6 Likes
Related Questions
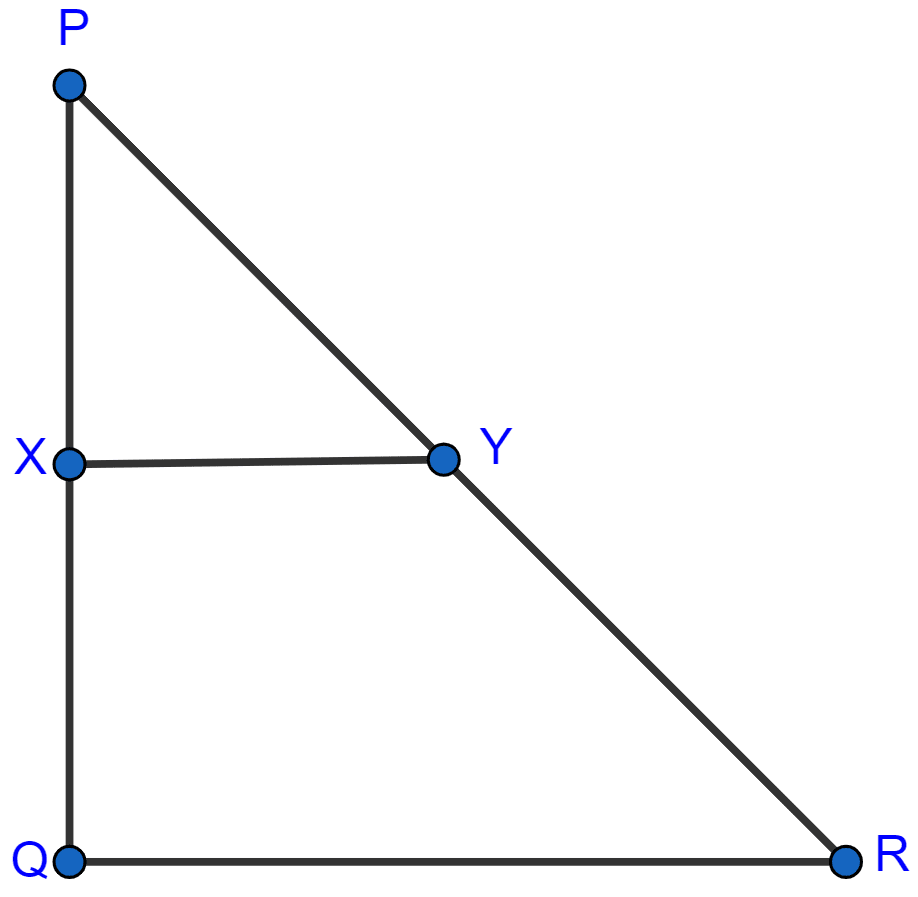
In the figure, given below, PQR is a right-angled triangle at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.
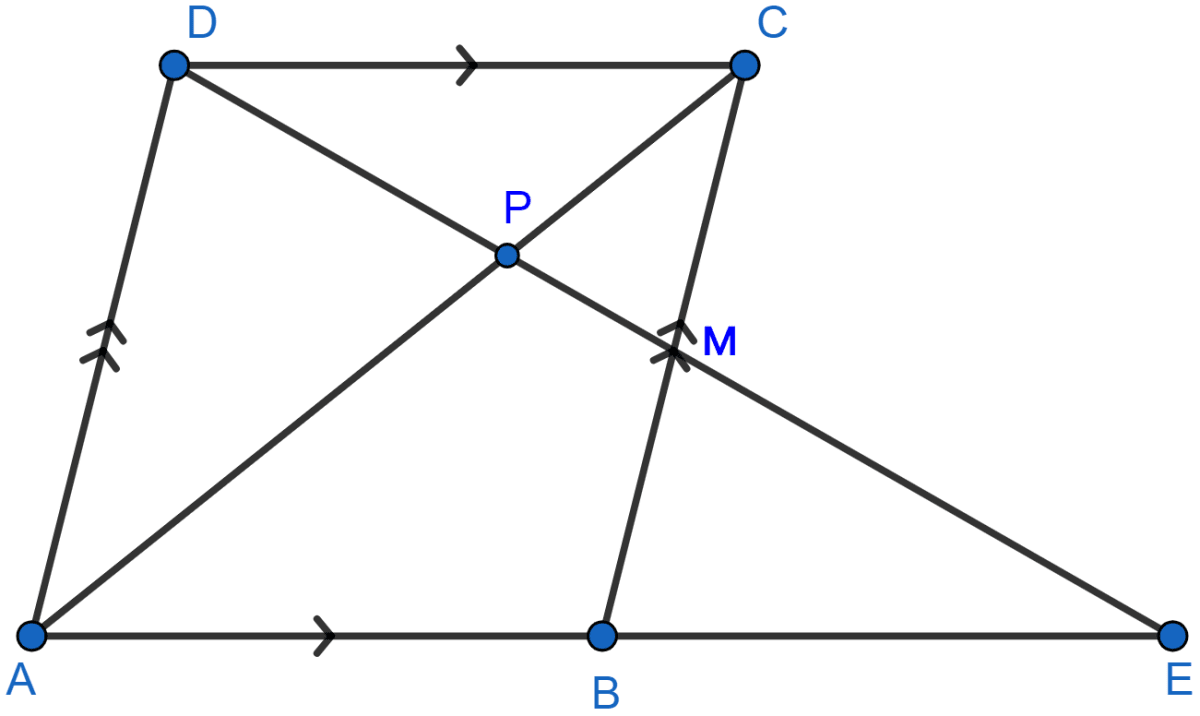
In the following figure, M is the mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2PD.
In the given figure, AE = 5 cm and EC = 7 cm, then area of △ ADE : area of △ ABC is :
5 : 7
7 : 5
25 : 144
144 : 25

If AD = 5 cm and BD = 2 cm, then area of △ ADE : area of trapezium DBCE is equal to :
5 : 2
2 : 5
24 : 25
25 : 24
