The figure alongside shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.

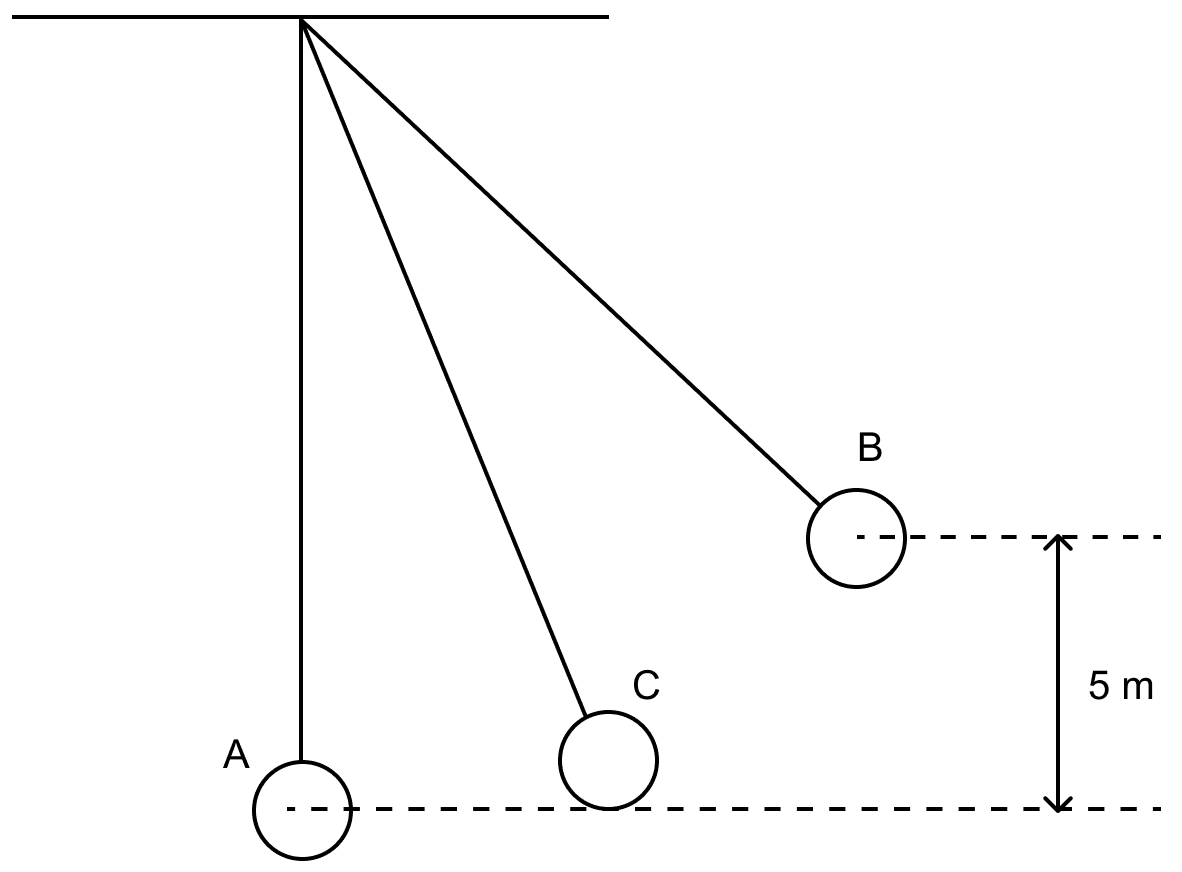
(i) What is the potential energy of the pendulum at the position B?

(ii) What is the total mechanical energy at point C?

(iii) What is the speed of the bob at the position A when released from B?

(Take g = 10 ms^-2 and there is no loss of energy.)

Given,

h = 5 m, m = 200 g = 0.2 kg, g = 10 ms^-2

(i) Potential energy U_B at B is given by

U_B = m x g x h

Substituting the values we get,

$U$B = 0.2 \times 10 \times 5 \\[0.5em] \Rightarrow UB = 10 J

Hence, the potential energy of the pendulum at the position B = 10 J

(ii) Total mechanical energy at point C = 10 J

The total mechanical energy is same at all points of the path due to conservation of mechanical energy.

(iii) At A, bob has only kinetic energy which is equal to potential energy at B,

Therefore,

$\dfrac{1}{2} \times m \times (v$A)^{2} = UB \\[0.5em] 0.5 \times 0.2 \times (vA)^{2} = 10 \\[0.5em] (vA)^{2} = \dfrac{10}{0.1} \\[0.5em] \Rightarrow vA = \sqrt{100} \\[0.5em] \Rightarrow vA = 10 \text{ m s}^{-1}