The coordinates of the vertex A of a square ABCD is (1, 2) and the equation of diagonal BD is x + 2y = 10. Find the equation of the other diagonal and the co-ordinates of the centre of the square.

The square is shown in the fig below:

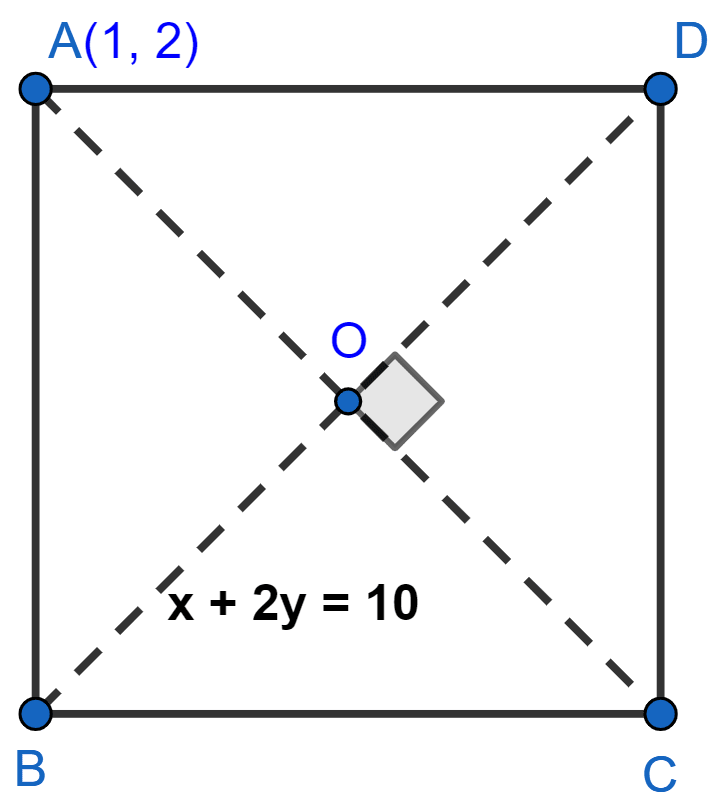
Given,

Equation of diagonal BD is x + 2y = 10

⇒ 2y = -x + 10

⇒ y = $-\dfrac{1}{2}x + \dfrac{10}{2}$

Comparing it with y = mx + c, we get :

Slope (m₁) = $-\dfrac{1}{2}$.

We know that,

Diagonals of a square are perpendicular to each other and product of slopes of perpendicular lines = -1.

Let slope of diagonal AC = m₂.

$\therefore m$2 \times -\dfrac{1}{2} = -1 \\[1em] \Rightarrow -m2 = -2 \\[1em] \Rightarrow m_2 = 2.

By point-slope form,

Equation of AC is y - y₁ = m(x - x₁)

⇒ y - 2 = 2(x - 1)

⇒ y - 2 = 2x - 2

⇒ 2x - 2 + 2 = y

⇒ y = 2x.

Since, center of the square is the point of intersection of its diagonals.

Solving,

x + 2y = 10 and y = 2x simultaneously, we get :

⇒ x + 2y = 10 …….(1)

⇒ y = 2x ………(2)

Substituting value of y from eq (2) in (1), we get :

⇒ x + 2(2x) = 10

⇒ x + 4x = 10

⇒ 5x = 10

⇒ x = $\dfrac{10}{5}$

⇒ x = 2.

⇒ y = 2x = 2(2) = 4.

Center = (2, 4).

Hence, equation of other diagonal is y = 2x and coordinates of circle = (2, 4).