Mathematics
The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. If an altitude of the smaller triangle is 3.5 cm, then the corresponding altitude of the bigger triangle is
9 cm
7 cm
6 cm
4.5 cm
Similarity
5 Likes
Answer
Let the altitude of bigger triangle be x cm.
We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding altitudes.
Hence, altitude of the bigger triangle is 4.5 cm.
Hence, Option 4 is the correct option.
Answered By
2 Likes
Related Questions
In the adjoining figure, DE || CA and D is a point on BD such that BD : DC = 2 : 1. The ratio of area of △ABC to area of △BDE is

4 : 1
9 : 1
9 : 4
3 : 2
If ABC and BDE are two equilateral triangles such that D is mid-point of BC, then the ratio of the areas of triangles ABC and BDE is
2 : 1
1 : 2
1 : 4
4 : 1
Given △ABC ~ △PQR, area of △ABC = 54 cm2 and area of △PQR = 24 cm2. If AD and PM are medians of △'s ABC and PQR respectively, and length of PM is 10 cm, then length of AD is
cm
cm
15 cm
22.5 cm
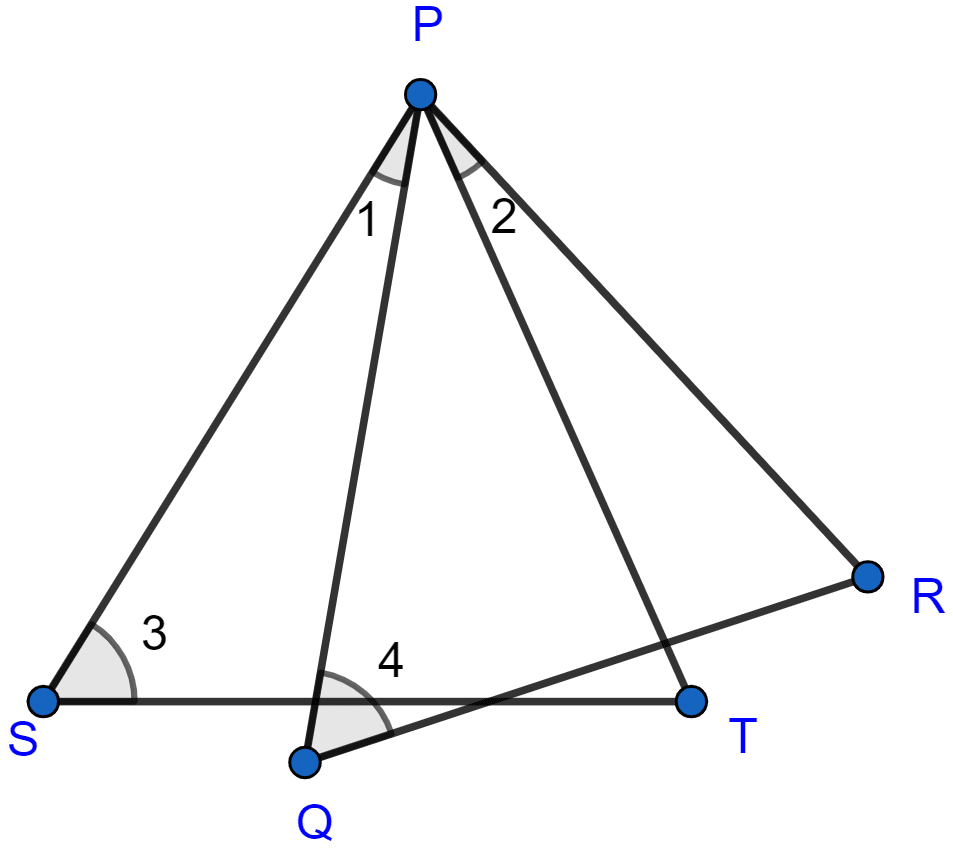
In the adjoining figure, ∠1 = ∠2 and ∠3 = ∠4. Show that PT × QR = PR × ST.