Mathematics
The angle of elevation of the top of a tower, from a point on the ground and at a distance of 150 m from its foot, is 30°. Find the height of the tower correct to one place of decimal.
Heights & Distances
46 Likes
Answer
Let MP be the tower of height h metres and O be the point on the ground 150 m away from the foot of the tower.
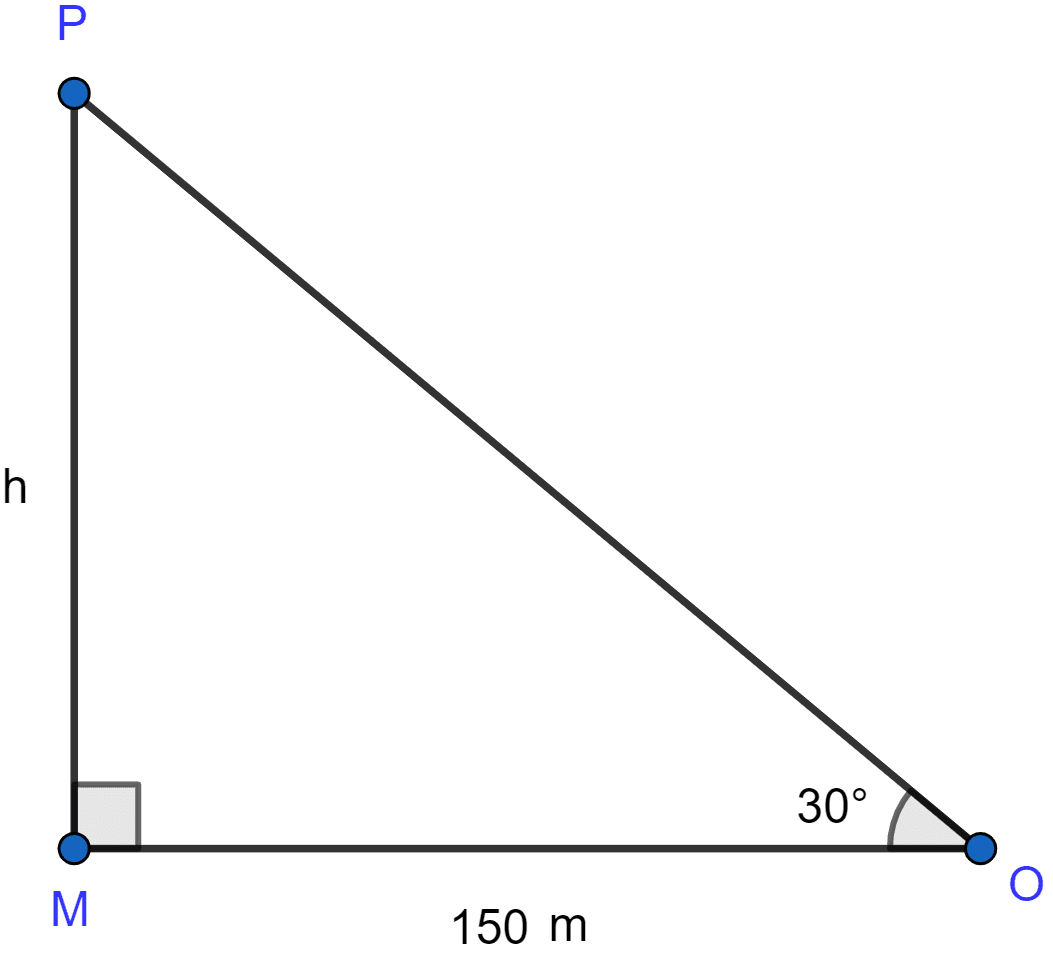
Then, the angle of elevation = ∠MOP = ∠30° (given).
In △OMP, ∠OMP = 90°.
From △OMP, we get
Hence, the height of the tower = 86.6 m.
Answered By
21 Likes
Related Questions
An electric pole is 10 metres high. If its shadow is metres in length, find the elevation of the sun.
A ladder is placed against a wall such that it just reaches the top of the wall. The foot of the ladder is 1.5 metres away from the wall and the ladder is inclined at an angle of 60° with the ground. Find the height of the wall.
What is the angle of elevation of sun when the length of shadow of a vertical pole is equal to its height?
From a point P on level ground, the angle of elevation of the top of a tower is 30°. If the tower is 100m high, how far is P from the foot of the tower ?